
分析 先设y1=k1x,y2=$\frac{{k}_{2}}{x-1}$(k1≠0,k2≠0),代入等式y=y1+y2中,并将两点代入列方程组求出字母系数,再写出函数关系式即可.
解答 解:设y1=k1x,y2=$\frac{{k}_{2}}{x-1}$(k1≠0,k2≠0),
∴y=y1+y2=k1x+$\frac{{k}_{2}}{x-1}$,
把当x=0时,y=1;当x=3时,y=0分别代入得:$\left\{\begin{array}{l}{1=-{k}_{2}}\\{0=3{k}_{1}+\frac{{k}_{2}}{3-1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{6}}\\{{k}_{2}=-1}\end{array}\right.$,
∴y与x之间的函数表达式为:y=$\frac{1}{6}$x-$\frac{1}{x-1}$;
故答案为:y=$\frac{1}{6}$x-$\frac{1}{x-1}$.
点评 本题考查了利用待定系数法求正比例函数和反比例函数的解析式,是一种组合函数,与单独的正比例函数类似,都是将函数上的点代入列方程组进行求解.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
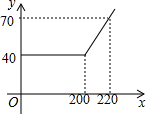 某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
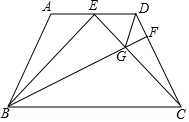 如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE
如图,在四边形ABCD中,AD∥BC,AB=DC,∠ABC=∠BCD,E为AD中点,连接BE,CE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20$\sqrt{5}$m | B. | 50m | C. | 50$\sqrt{3}$m | D. | 100m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com