
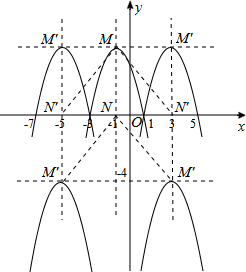
|
|
| b |
| 2a |
| -2 |
| 2×(-1) |


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
| 几何中,平行四边形、矩形、菱形、正方形和等腰梯形都是特殊的四边形,大家对于它们的性质都非常熟悉,生活中还有一种特殊的四边形--筝形.所谓筝形,它的形状与我们生活中风筝的骨架相似. 定义:两组邻边分别相等的四边形,称之为筝形,如图,四边形ABCD是筝形,其中AB=AD,CB=CD 判定:①两组邻边分别相等的四边形是筝形 ②有一条对角线垂直平分另一条对角线的四边形是筝形 显然,菱形是特殊的筝形,就一般筝形而言,它与菱形有许多相同点和不同点 | 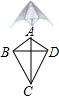 |
查看答案和解析>>
科目:初中数学 来源: 题型:
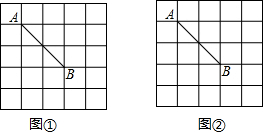 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.一条线段AB的两端点落在格点(即小正方形的顶点)上,且长度为2
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.一条线段AB的两端点落在格点(即小正方形的顶点)上,且长度为2| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
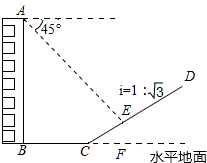 如图,一楼房AB后有一假山,其坡度为i=1:
如图,一楼房AB后有一假山,其坡度为i=1:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com