
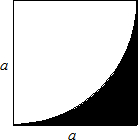
 (1)如图,用含a的代数式表示图中阴影部分的面积;
(1)如图,用含a的代数式表示图中阴影部分的面积;科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 =
=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.
(2013•桥西区模拟)注意:为了使同学们更好地解答本题,下面提供了一种解题思路,你可以依照这个思路填空,并完成本题解答的全过程.如果你选用其他的解题方案,此时,不必填空,只需按照解答题的一般要求,进行解答即可.查看答案和解析>>
科目:初中数学 来源: 题型:
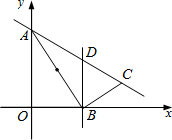 已知A(0,6),点B(t,0)是x轴正半轴上的一个动点,连接AB,作BC⊥AB,且BC:AB=1:2.又BD⊥x轴交直线AC于点D.
已知A(0,6),点B(t,0)是x轴正半轴上的一个动点,连接AB,作BC⊥AB,且BC:AB=1:2.又BD⊥x轴交直线AC于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com