
(本题满分15分)如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连结PQ.点P,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
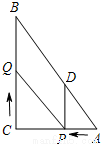
(1)直接用含t的代数式分别表示:QB= ,PD= ;
(2)是否存在t的值,使四边形PDBQ为平行四边形?若存在,求出t的值;若不存在,说明理由;
(3)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
【解析】
(1)QB=12-2t,PD=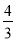 t。
t。
∵PD∥BC,当PD=BQ时四边形PDBQ为平行四边形,
即12-2t=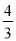 t,解得:t=
t,解得:t=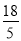 (秒)(或t=3.6秒)
(秒)(或t=3.6秒)
∴存在t的值,使四边形PDBQ为平行四边形。
∵t=3.6时,BQ=PD=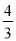 t=4.8,由△ABC∽△ADP,∴AD=
t=4.8,由△ABC∽△ADP,∴AD=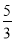 t=6,BD=15-6=9,
t=6,BD=15-6=9,
∴BD≠PD,∴不存在t使四边形PDBQ为菱形。
设点Q的速度为每秒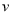 个单位长度
个单位长度
则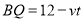 ,
,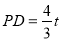 ,
,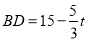
要使四边形PDBQ为菱形,则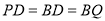
当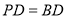 时,即
时,即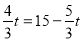 ,解得:
,解得: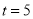
当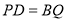 ,
,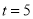 时,即
时,即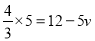 ,解得:
,解得: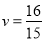
∴当点Q的速度为每秒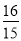 个单位长度时,经过
个单位长度时,经过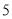 秒,四边形PDBQ是菱形
秒,四边形PDBQ是菱形
【解析】
试题分析:(1)根据题意得:CQ=2t,PA=t,由Rt△ABC中,∠C=90°,AC=9,BC=12,PD∥BC,即可得tanA=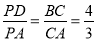 ,则可求得QB与PD的值;(2)由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形,据此列出方程,解得即可;(3)利用(2)中所求,即可求得此时DP与BD的长,由BD≠PD,可判定?PDBQ不能为菱形;然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程即可求得答案.
,则可求得QB与PD的值;(2)由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形,据此列出方程,解得即可;(3)利用(2)中所求,即可求得此时DP与BD的长,由BD≠PD,可判定?PDBQ不能为菱形;然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程即可求得答案.
考点:相似三角形的判定与性质;平行四边形的判定与性质;菱形的判定与性质.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2014-2015学年河北省深州市九年级上学期第三次月考数学试卷(解析版) 题型:填空题
如图,使一长为4 ,宽为3
,宽为3 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为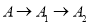 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时,点A共走过的路径长是 cm.
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时,点A共走过的路径长是 cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:填空题
在一个不透明的盒子中装有2个白球,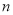 个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为
个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是白球的概率为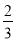 ,则
,则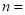 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上
C.在一个装着白球和黑球的袋中摸球,摸出红球是随机事件
D.掷一枚质地均匀的骰子,朝上一面的点数是7是确定事件
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:解答题
正方形网格中,小格的顶点叫做格点。三个顶点都在网格格点上的三角形叫做格点三角形。小华已在左边的正方形网格中作出一个格点三角形。请你在其他两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:选择题
如图,直线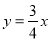 与双曲线
与双曲线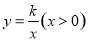 交于点A。将直线
交于点A。将直线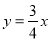 向右平移6个单位后,与双曲线
向右平移6个单位后,与双曲线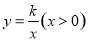 交于点B,与
交于点B,与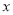 轴交于点C,若
轴交于点C,若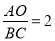 ,则
,则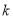 的值为( )
的值为( )
A.12 B.14 C.18 D.24
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市小片区九年级上学期半期考试数学试卷(解析版) 题型:填空题
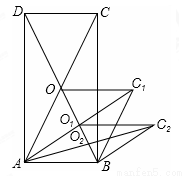
如图,矩形ABCD的面积为20cm2,对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为_____________
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:选择题
将抛物线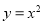 向下平移3个单位,则得到的抛物线解析式为
向下平移3个单位,则得到的抛物线解析式为
A. B.
B. C.
C.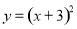 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com