
 如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$.
如图,在四边形ABCD中,AD∥BC,∠C=90°,E为CD上一点,分别以EA,EB为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处.若AD=2,BC=3,则EF的长为$\sqrt{6}$. 分析 先根据折叠的性质得DE=EF,CE=EF,AF=AD=2,BF=CB=3,则DC=2EF,AB=5,再作AH⊥BC于H,由于AD∥BC,∠B=90°,则可判断四边形ADCH为矩形,所以AH=DC=2EF,HB=BC-CH=BC-AD=1,然后在Rt△ABH中,利用勾股定理计算出AH=2$\sqrt{6}$,所以EF=$\sqrt{6}$.
解答 解∵分别以AE,BE为折痕将两个角(∠D,∠C)向内折叠,点C,D恰好落在AB边的点F处,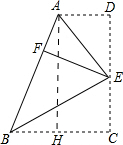
∴DE=EF,CE=EF,AF=AD=2,BF=CB=3,
∴DC=2EF,AB=5,
作AH⊥BC于H,
∵AD∥BC,∠C=90°,
∴四边形ADCH为矩形,
∴AH=DC=2EF,HB=BC-CH=BC-AD=1,
在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=2$\sqrt{6}$,
∴EF=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).
在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是( )| A. | 2015π | B. | 3019.5π | C. | 3018π | D. | 3024π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
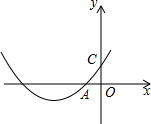 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )| A. | ac+1=b | B. | ab+1=c | C. | bc+1=a | D. | 以上都不是 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com