
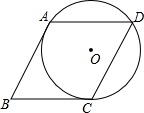
 如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.
如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数. 分析 连接OA、OC、OB.由切线的性质可知∠OAB=90°,然后证明△AOB≌△COB,从而得到∠OCB=∠OAB=90°,于是得到∠ABC+∠AOC=180°然后根据圆周角定理和菱形的性质可知∠AOC=2∠ABC,从而可求得∠AOC=60°.
解答 解:如图所示:连接OA、OC、OB.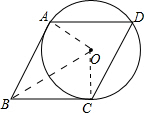
∵BA是圆O的切线,
∴OA⊥AB.
∴∠BAO=90°.
∵四边形ABCD是菱形,
∴AB=BC,∠ABC=∠ADC.
在△AOB和△COB中,
$\left\{\begin{array}{l}{AB=CB}\\{OA=OC}\\{OB=OB}\end{array}\right.$,
∴△AOB≌△COB.
∴∠OCB=∠OAB=90°.
∴∠ABC+∠AOC=180°.
又∵∠ADC=$\frac{1}{2}$∠AOC,
∴∠AOC=2∠ABC.
∴3∠AOC=180°.
∴∠AOC=60°.
点评 本题主要考查的是切线的性质、菱形的性质、全等三角形的性质和判定,证得∠AOC=2∠ABC、∠ABC+∠AOC=180°是解题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
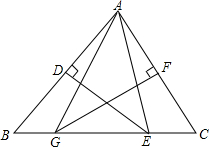 如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长?
如图,△ABC中,BC=12,∠BAC=70°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G.能否求出∠EAG的度数和△AEG的周长?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.
如图为一个正方体的展开图,图中已标出三个面在正方体中的位置f表示前面,r表示右面,d表示下面.试判定另外三个面a、b、c在正方体中的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
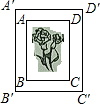 如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?
如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?
已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{31}{36}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com