
 如图,点H是线段BC的中点,∠ABH=∠DCH=90°,AH=DH,则△ABH≌________,依据是________.
如图,点H是线段BC的中点,∠ABH=∠DCH=90°,AH=DH,则△ABH≌________,依据是________. 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
 (1)化简:(a-
(1)化简:(a-| 1 |
| a |
| a2-2a+1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
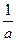 )÷
)÷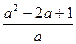 ;
;
查看答案和解析>>
科目:初中数学 来源:2010年浙江省初中毕业生学业考试模拟试卷数学卷 题型:解答题
(每小题8分,共16分)
(1)化简:(a-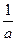 )÷
)÷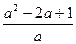 ;
;
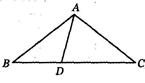
(2)已知:在△ABC中,AB=AC.
①设△ABC的周长为7,BC=y,AB=x(2≤x≤3).写出y关于x的函数关系式;
②如图,点D是线段BC上一点,连结AD,若∠B=∠BAD,求证:△BAC∽△BDA.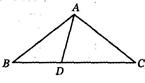
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com