
| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
| 5 |
| 2 |
| 10 |
| 12 |
| 7 |
| 9 |
| 7 |
| 9 |
| 7 |
| 19 |
| 7 |
| 19 |
| 7 |
-7+
| ||
| 2 |
-7-
| ||
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
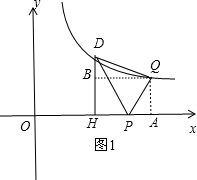 解:∵3×4=12,
解:∵3×4=12,| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
| 12 |
| x |
| 22+12 |
| 5 |
| 2 |
| 10 |
(
|
| 12 |
| 7 |
| 12 |
| 7 |
| 9 |
| 7 |
| 9 |
| 7 |
| 9 |
| 7 |
| 19 |
| 7 |
| 19 |
| 7 |
-7+
| ||
| 2 |
-7-
| ||
| 2 |
-7+
| ||
| 2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
| 19 |
| 7 |
1+
| ||
| 2 |
| k |
| x |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
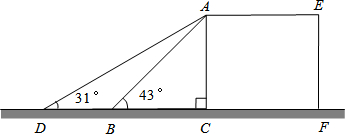
 如图,一个梯子AB长2.5m,顶端A靠在墙OB上,这时梯子下端A与墙角O距离为0.7m,梯子滑动后停在A′B′的位置上,测得BB′长为0.4m,求梯子底端A滑动了多少米.
如图,一个梯子AB长2.5m,顶端A靠在墙OB上,这时梯子下端A与墙角O距离为0.7m,梯子滑动后停在A′B′的位置上,测得BB′长为0.4m,求梯子底端A滑动了多少米.查看答案和解析>>
科目:初中数学 来源: 题型:
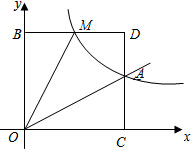 如图,反比例函数y=
如图,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
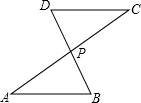 如图,AC与BD交于点P,AP=CP,从以下四个论断①AB=CD,②BP=DP,③∠B=∠D,④∠A=∠C中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是
如图,AC与BD交于点P,AP=CP,从以下四个论断①AB=CD,②BP=DP,③∠B=∠D,④∠A=∠C中选择一个论断作为条件,则不一定能使△APB≌△CPD的论断是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com