
已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y轴正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,如图所示.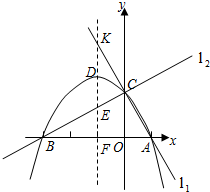
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.

KD=DE=EF;点M的坐标分别为(﹣2, ),(﹣1,
),(﹣1, )时,
)时,
△MCK为等腰三角形.
解析试题分析:(1)解法1:由题意易知:△BOC∽△COA,
∴ ,即
,即 ,∴
,∴ ,
,
∴点C的坐标是(0, ), 2分
), 2分
由题意,可设抛物线的函数解析式为 ,
,
把A(1,0),B(﹣3,0)的坐标分别代入 ,
,
得 ,解这个方程组,得
,解这个方程组,得 ,
,
∴抛物线的函数解析式为 . .4分
. .4分
(2)解法1:截得三条线段的数量关系为KD=DE=EF.
理由如下:
可求得直线l1的解析式为 ,
,
直线l2的解析式为 ,
,
抛物线的对称轴为直线x=-1, 6分
由此可求得点K的坐标为(﹣1, ),
),
点D的坐标为(﹣1, ),点E的坐标为(﹣1,
),点E的坐标为(﹣1, ),点F的坐标为(﹣1,0).
),点F的坐标为(﹣1,0).
∴KD= ,DE=
,DE= ,EF=
,EF= ,
,
∴KD=DE=EF. 8分
(3)当点M的坐标分别为(﹣2, ),(﹣1,
),(﹣1, )时,△MCK为等腰三角形.
)时,△MCK为等腰三角形.
理由如下:
(i)连接BK,交抛物线于点G,易知点G的坐标为(﹣2, ),
),
又∵点C的坐标为(0, ),则GC∥AB,
),则GC∥AB,
∵可求得AB=BK=4,且∠ABK=60°,即△ABK为正三角形,
∴△CGK为正三角形
∴当l2与抛物线交于点G,即l2∥AB时,符合题意,此时点M1的坐标为(﹣2, ), 10分
), 10分
(ii)连接CD,由KD= ,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形,
,CK=CG=2,∠CKD=30°,易知△KDC为等腰三角形,
∴当l2过抛物线顶点D时,符合题意,此时点M2坐标为(﹣1, ), .12分
), .12分
(iii)当点M在抛物线对称轴右边时,只有点M与点A重合时,满足CM=CK,
但点A、C、K在同一直线上,不能构成三角形,
综上所述,当点M的坐标分别为(﹣2, ),(﹣1,
),(﹣1, )时,
)时,
△MCK为等腰三角形.
考点:相似三角形的判定
点评:解答本题的的关键是熟练掌握有两组角对应相等的两个三角形相似;两组边对应成比例且夹角相等的三角形相似


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
 B两点,两直线相交于点A.
B两点,两直线相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知两直线l1,l2分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点D,如图所示.
已知两直线l1,l2分别经过点A(3,0),点B(-1,0),并且当两直线同时相交于y负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点D,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(2012•成华区一模)已知两直线l1、l2分别经过点A(3,0),点B(-1,0),并且当两条直线同时相交于y轴负半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
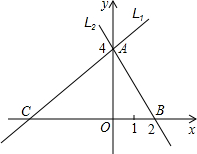
 已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A.
已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com