
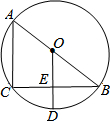
 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.分析 (1)根据直角所对的圆周角是直角、垂径定理写出结论;
(2)根据勾股定理求出DE的长,设⊙O的半径为R,根据勾股定理列出关于R的方程,解方程得到答案.
解答 解:(1)∵AB是⊙O的直径,
∴∠C=90°,
∵OD⊥CB,
∴CE=BE,$\widehat{CD}$=$\widehat{BD}$,
则三个不同类型的正确结论:∠C=90°;CE=BE;$\widehat{CD}$=$\widehat{BD}$;
(2)∵OD⊥CB,
∴CE=BE=$\frac{1}{2}$BC=4,又DE=2,
∴OE2=OB2-BE2,
设⊙O的半径为R,则OE=R-2,
∴R2=(R-2)2+42,
解得R=5.
答:⊙O的半径为5.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
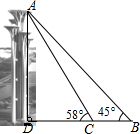 奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com