

 ;
; ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
,并通过操作、观察,直接写出BG长度的取值范围(不必说理); ),探索2PO+PM的最小值.
),探索2PO+PM的最小值.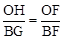 ;由EF∥AB,得
;由EF∥AB,得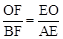 .所以
.所以 。
。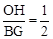 ,根据①中的结论,易得
,根据①中的结论,易得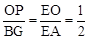 ,故问题得证。
,故问题得证。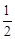 ∠COA=45°。
∠COA=45°。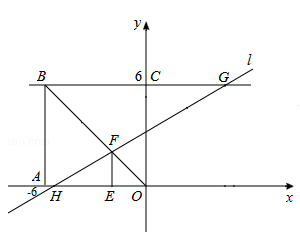
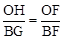 。
。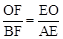 。
。 。
。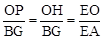 ,
,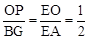 。
。 ,
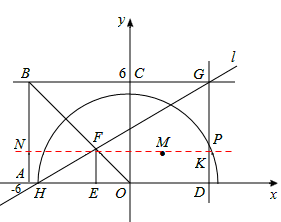
,


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:不详 题型:填空题
 ,0)、B(0,4),对△OAB连续作旋转变换,
,0)、B(0,4),对△OAB连续作旋转变换,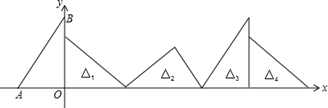
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.关于x轴对称 |
| B.关于y轴对称 |
| C.关于原点对称 |
| D.将原图形向x轴负方向平移了1个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com