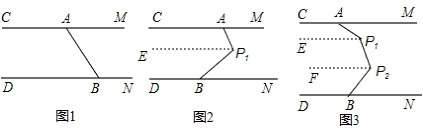
解:(1)∵CM∥DN.
∴∠CAB+∠ABD=180°;
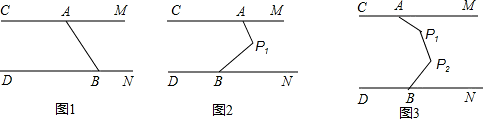
(2)点P
1作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP
1B+∠P
1BD=180°,
∴∠CAP
1+∠AP
1B+∠P
1BD=∠AP
1E+∠CAB+∠EP
1B+∠P
1BD=180°+180°=360°;
(3)过点P
1、P
2作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP
1P
2+∠P
1P
2F=180°,∠FP
2B+∠P
2BD=180°,
∴∠CAP
1+∠AP
1P
2+∠P
1P
2B+∠P
2BD=∠AP
1E+∠CAB+∠EP
1P
2+∠P
1P
2F+∠FP
2B+∠P
2BD=3×180°=540°;
(4)∠CAP
1+∠AP
1P
2+…∠P
5BD=6×180°=1080°.
分析:(1)直接利用平行线的性质得到两个同旁内角的和即可;
(2)过点P
1作平行于CM和DN的平行线,利用同旁内角的和为180°即可得到答案;
(3)过点P
1、P
2作平行于CM和DN的平行线,利用同旁内角的和为180°即可得到答案;
(4)用上面题目得到的规律直接写出答案即可.
点评:本题考查了平行线的性质,解题的关键是正确的作出辅助线,利用平行线的性质进行证明.

 解:(1)∵CM∥DN.
解:(1)∵CM∥DN.

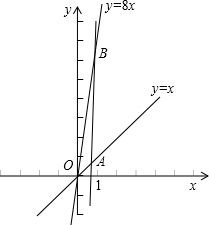 如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0 ).若直线AB为一次函数y=kx+m的图象,则当