
 x-4,并且与x轴、y轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,则该圆运动的时间为( )
x-4,并且与x轴、y轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,则该圆运动的时间为( )
 x-4可以求出与x轴、y轴的交点A(3,0)、B(0,-4)坐标,再根据勾股定理可得AB=5,当C在B上方,根据直线与圆相切时知道C到AB的距离等于1.5,然后利用三角函数可得到CB,最后即可得到C运动的距离和运动的时间;同理当C在B下方,利用题意的方法也可以求出C运动的距离和运动的时间.
x-4可以求出与x轴、y轴的交点A(3,0)、B(0,-4)坐标,再根据勾股定理可得AB=5,当C在B上方,根据直线与圆相切时知道C到AB的距离等于1.5,然后利用三角函数可得到CB,最后即可得到C运动的距离和运动的时间;同理当C在B下方,利用题意的方法也可以求出C运动的距离和运动的时间.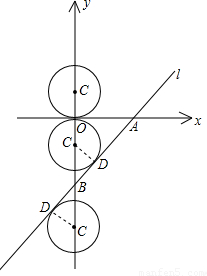 解:如图,∵x=0时,y=-4,
解:如图,∵x=0时,y=-4, =2.5;
=2.5;

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年河南省周口市扶沟县中考数学模拟试卷(一)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年浙江省衢州市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2007年浙江省衢州市中考数学试卷(解析版) 题型:选择题
 x-4,并且与x轴、y轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,则该圆运动的时间为( )
x-4,并且与x轴、y轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当⊙C与直线l相切时,则该圆运动的时间为( )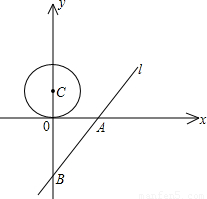
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com