
| 三边a、b、c | a+b-c | 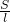 |
| 3、4、5 | 2 | |
| 5、12、13 | 4 | |
| 8、15、17 | 6 |
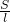 =______,(用含有m的代数式表示);
=______,(用含有m的代数式表示); ab,周长l=a+b+c,故当a、b、c三边分别为3、4、5时,S=
ab,周长l=a+b+c,故当a、b、c三边分别为3、4、5时,S= ×3×4=6,l=3+4+5=12,故
×3×4=6,l=3+4+5=12,故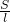 =
= ,同理将其余两组数据代入可得
,同理将其余两组数据代入可得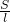 为1,
为1, .
. ,1,
,1,
 .
. ab,
ab, .
. ab,周长l=a+b+c,分别将3、4、5,5、12、13,8、15、17三组数据代入两式,可求出
ab,周长l=a+b+c,分别将3、4、5,5、12、13,8、15、17三组数据代入两式,可求出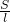 的值;
的值;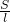 =
= ;
; ab可得出:lm=4s,即
ab可得出:lm=4s,即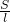 =
= .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com