
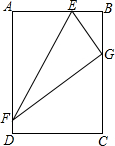
 如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )
如图,矩形ABCD的边AB有一点E,AE:EB=3:2,DA边上有点F,且EF=18,将矩形沿EF对折后,点A落在边BC上的点G,则AB为( )| A. | 3$\sqrt{6}$ | B. | 5$\sqrt{6}$ | C. | 5$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
分析 由AE:EB=3:2,假设出AE=3x,EB=2x,从而可以表示出FG=AF,BG的长,作FH⊥BC于H,可以得出△FGH∽△GEB,利用相似三角形性质可以求出AB的长.
解答 解:设AE=3x,EB=2x,
则FG=AF=$\sqrt{1{8}^{2}-9{x}^{2}}$=$\sqrt{324-9{x}^{2}}$,
∵EG=AE=3x,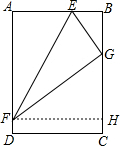
∴BG=$\sqrt{{EG}^{2}{-BE}^{2}}$=$\sqrt{5}$x,
作FH⊥BC交BC于点H,则△FGH∽△GEB,
∴$\frac{FG}{GE}=\frac{FH}{GB}$,即$\frac{\sqrt{324-9{x}^{2}}}{3x}=\frac{5x}{\sqrt{5}}$,
解得:x=±$\sqrt{6}$(负值舍去),
∴AB=5x=5$\sqrt{6}$;
故选:B.
点评 此题主要考查了折叠变换的性质,矩形的性质以及相似三角形的判定与性质等知识;得出AF=FG和证明△FGH∽△GEB是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
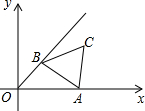 如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{3}$ | D. | 1+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com