Question

11．如图，为测悬崖的高AB，某小组在平地点C处测得点B在北偏西60°方向．沿正西方向行走50m，在点D处测得点B在北偏西45°方向，并测得点A的仰角为60°．求悬崖的高．（若有根号不用取近似值．AB为竖直方向，B，C，D在同一水平面．）

Answer 1

分析 先作BE⊥CD于E，设BE=DE=x，根据CE=DE+CD，得到$\sqrt{3}$x=x+50，求得BE=DE=25（$\sqrt{3}$+1），BD=$\sqrt{2}$x=25（$\sqrt{6}$+$\sqrt{2}$），在Rt△ABD中，根据∠ADB=60°，即可得到AB=BD×tan60°，据此可得AB的长．

解答 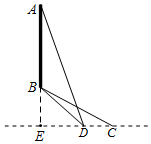解：如图，作BE⊥CD于E，
由题可得，∠BDE=45°，∠BCE=30°，CD=50，
∴BE=DE，
设BE=DE=x，
Rt△BCE中，CE=$\frac{BE}{tan30°}$=$\sqrt{3}$x，
∵CE=DE+CD，
∴$\sqrt{3}$x=x+50，
解得x=25（$\sqrt{3}$+1），
∴BE=DE=25（$\sqrt{3}$+1），
∴Rt△BDE中，BD=$\sqrt{2}$x=25（$\sqrt{6}$+$\sqrt{2}$），
∵在Rt△ABD中，∠ADB=60°，
∴AB=BD×tan60°=$\sqrt{3}$BD=25（3$\sqrt{2}$+$\sqrt{6}$）=75$\sqrt{2}$+25$\sqrt{6}$，
∴悬崖的高AB为（75$\sqrt{2}$+25$\sqrt{6}$）米．

点评 本题主要考查了解直角三角形的应用，解决问题的关键是作辅助线构造直角三角形，解题时注意：所画的示意图为立体图形，△ABD为直角三角形且∠ABD=90°，∠ADB为仰角．