Question

16．如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax²-10ax+16a（a≠0）交x轴于A、B两点，抛物线的顶点为D，对称轴与x轴交于点H，且AB=2DH．
（1）求a的值；
（2）点P是对称轴右侧抛物线上的点，连接PD，PQ⊥x轴于点Q，点N是线段PQ上的点，过点N作NF⊥DH于点F，NE⊥PD交直线DH于点E，求线段EF的长；
（3）在（2）的条件下，连接DN、DQ、PB，当DN=2QN（NQ＞3），2∠NDQ+∠DNQ=90°时，作NC⊥PB交对称轴左侧的抛物线于点C，求点C的坐标．

Answer 1

分析 （1）根据y=ax²-10ax+16a可以求得当y=0时，x的值，从而可以求得点A、B的坐标，由抛物线的顶点为D，对称轴与x轴交于点H，且AB=2DH，从而可以求得a的值；
（2）根据已知条件作出相应的图形，然后根据题意题目中的数量关系，通过灵活变形可以求得EF的长；
（3）根据题意可以画出相应的图形，然后根据题目中的关系，利用三角形相似，灵活变化可以求得点C的坐标．

解答 解：（1）令y=0，
∵a≠0，
∴x²-10x+16=0，得x=2或x=8，
∴点A（2，0），B（8，0），
∴AB=8-2=6，
∵AB=2DH，
∴DH=3，
∵OH=2+$\frac{1}{2}AB=2+3=5$，
∴D（5，-3），
∴-3=a×5²-10a×5+16a，得a=$\frac{1}{3}$；
（2）如图1，过点D作PQ的垂线，交PQ的延长线于点M，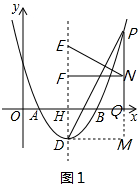
∵NE⊥PD，
∴∠DPN+∠PNE=90°，
∵NF⊥DE，
∴∠FEN+∠FNE=90°，
又∵DH⊥x轴，PQ⊥x轴，
∴DE∥PQ，
∴∠FEN=∠PNE，
∴∠DPM=∠ENF，
∴△EFN∽△DMP，
∴$\frac{EF}{DM}=\frac{FN}{MP}$，
设点P（t，$\frac{1}{3}{t}^{2}-\frac{10}{3}t+\frac{16}{3}$），
则FN=DM=t-5，PM=$\frac{1}{3}{t}^{2}-\frac{10}{3}t+\frac{16}{3}$+3，
∴$\frac{EF}{t-5}=\frac{t-5}{\frac{1}{3}{t}^{2}-\frac{10}{3}t+\frac{16}{3}+3}$，
解得，EF=3；
（3）如图2，作QG⊥DN于点G，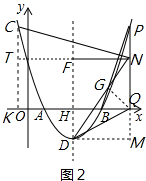
∵DF∥PQ，
∴∠FDN=∠DNQ，
∵2∠NDQ+∠DNQ=90°，
∴2∠NDQ+∠FDN=90°，
∵∠FDM=90°，
∴∠NDM=2∠NDQ，
∴∠NDQ=∠MDQ，
∴QG=QM=DH=3，
设QN=m，则DN=2m，
∵sin∠DNM=$\frac{DM}{DN}$，sin∠QNG=$\frac{GQ}{NQ}$，sin∠DNM=sin∠QNG，
∴$\frac{DM}{2m}=\frac{3}{m}$，得DM=6=DG，
∴OQ=5+6=11，
∴点P的纵坐标是：$\frac{1}{3}×（1{1}^{2}-10×11+16）=9$，
∴点P（11，9），
∵NG=DN-DG=2m-6，在Rt△NGQ中，QG²+NG²=QN²，
∴3²+（2m-6）²=m²，
解得，m=3（舍去）或m=5，
设点C的坐标为（n，$\frac{1}{3}{n}^{2}-\frac{10}{3}n+\frac{16}{3}$），作CK⊥x轴于点K，作NF⊥CK于点K，
则CT=$\frac{1}{3}{n}^{2}-\frac{10}{3}n+\frac{16}{3}-5$，NT=11-n，
∵P（11，9），则BQ=11-8=3，PQ=9，
∵CN⊥PB，PQ∥CK，PQ⊥x轴，
∴△CTN∽△BQP，
∴$\frac{CT}{BQ}=\frac{NT}{PQ}$，
即$\frac{\frac{1}{3}{n}^{2}-\frac{10}{3}n+\frac{16}{3}-5}{3}=\frac{11-n}{9}$，
解得，n=-1或n=10（舍去），
∴点C（-1，9）．

点评 本题考查二次函数综合题，解题的关键是根据题意画出相应的图形，利用数形结合的思想解答，找出所求问题需要的条件，注意题目中的条件，如NQ＞3．