Question

已知：直线y=x+6交x、y轴于A、C两点，经过A、O两点的抛物线y=ax²+bx（a＜0）的顶点在直线AC上．
（1）求A、C两点的坐标；
（2）求出抛物线的函数关系式；
（3）以B点为圆心，以AB为半径作⊙B，将⊙B沿x轴翻折得到⊙D，试判断直线AC与⊙D的位置关系，并求出BD的长；
（4）若E为⊙B劣弧OC上一动点，连接AE、OE，问在抛物线上是否存在一点M，使∠MOA：∠AEO=2：3？若存在，试求出点M的坐标；若不存在，试说明理由．

Answer 1

解：（1）A（-6，0），C（0，6）

（2）∵抛物线y=ax²+bx（a＜0）经过A（-6，0），0（0，0）．
∴对称轴x=-=-3，b=6a…①
当x=-3时，代入y=x+6得y=-3+6=3，
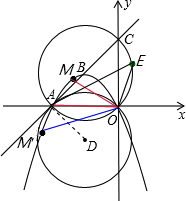
∴B点坐标为（-3，3）．
∵点B在抛物线y=ax²+bx上，
∴3=9a-3b…②
结合①②解得a=-，b=-2，
∴该抛物线的函数关系式为y=-x²-2x．

（3）相切
理由：连接AD，
∵AO=OC
∴∠ACO=∠CAO=45°
∵⊙B与⊙D关于x轴对称
∴∠BAO=∠DAO=45°
∴∠BAD=90°
又∵AD是⊙D的半径，
∴AC与⊙D相切．
∵抛物线的函数关系式为y=-x²-2x，
∴函数顶点坐标为（-3，3），
由于D、B关于x轴对称，
则BD=3×2=6．

（4）存在这样的点M．
设M点的坐标为（x，y）
∵∠AEO=∠ACO=45°
而∠MOA：∠AEO=2：3
∴∠MOA=30°
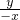
当点M在x轴上方时，=tan30°=，
∴y=-x．
∵点M在抛物线y=-x²-2x上，
∴-x=-x²-2x，
解得x=-6+，x=0（不合题意，舍去）
∴M（-6+，-1+2）．
当点M在x轴下方时，=tan30°=，
∴y=x，
∵点M在抛物线y=-x²-2x上．
∴x=-x²-2x，
解得x=-6-，x=0（不合题意，舍去）．
∴M（-6-，-1-2），
∴M的坐标为（-6+，-1+2）或（-6-，-1-2）．
分析：（1）根据过A、C两点的直线的解析式即可求出A，C的坐标．
（2）根据A，O的坐标即可得出抛物线的对称轴的解析式，然后将A点坐标代入抛物线中，联立上述两式即可求出抛物线的解析式．
（3）直线与圆的位置关系无非是相切与否，可连接AD，证AD是否与AC垂直即可．由于B，D关于x轴对称，那么可得出∠CAO=∠DAO=45°，因此可求出∠DAB=90°，即DA⊥AC，因此AC与圆D相切．
（4）根据圆周角定理可得出∠AEO=45°，那么∠MOA=30°，即M点的纵坐标的绝对值和横坐标的绝对值的比为tan30°，由此可得出x，y的比例关系式，然后联立抛物线的解析式即可求出M点的坐标．（要注意的是本题要分点M在x轴上方还是下方两种情况进行求解）
点评：本题着重考查了待定系数法求二次函数解析式、图形旋转变换、切线的判定、圆周角定理等知识点，综合性强，考查学生分类讨论，数形结合的数学思想方法．