
【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90° 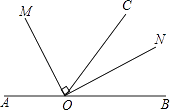
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
【答案】
(1)解:∵OM平分∠AOC,
∴∠AOM= ![]() ∠AOC=55°,
∠AOC=55°,
∴∠BOM=∠AOB﹣∠AOM=180°﹣55°=125°
(2)解:ON是∠BOC的角平分线.理由如下:
∵∠MON=90°,∠AOB=180°,
∴∠MOC+∠CON=90°,∠AOM+∠BON=90°,
又由(1)可知∠AOM=∠MOC,
∴∠CON=∠BON,
即ON是∠BOC的角平分线
【解析】(1)根据角的平分线的定义求得∠AOM的度数,然后根据邻补角的定义求得∠BOM的度数;(2)首先根据∠MON=90°,∠AOB=180°,得出∠MOC+∠CON=90°,∠AOM+∠BON=90°,又∠AOM=∠MOC,根据等角的余角相等即可得到ON是∠BOC的角平分线.
【考点精析】根据题目的已知条件,利用角的平分线和角的运算的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
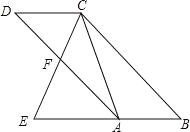
【题目】如图,已知:四边形ABCD是平行四边形,点E在边BA的延长线上,CE交AD于点F,∠ECA=∠D
(1)求证:△EAC∽△ECB;
(2)若DF=AF,求AC:BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
测试项目 | 测试成绩(分) | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
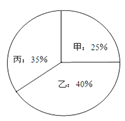
(1)请算出三人的民主评议得分.
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4︰3︰3![]() 的比例确定个人成绩,那么谁将被录用?
的比例确定个人成绩,那么谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是BC延长线上的一点,线段BD的垂直平分线EG交AB于点E,交BD于点G. 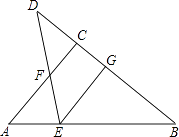
(1)当∠B=30°时,AE和EF有什么关系?请说明理由;
(2)当点D在BC延长线上(CD<BC)运动时,点E是否在线段AF的垂直平分线上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com