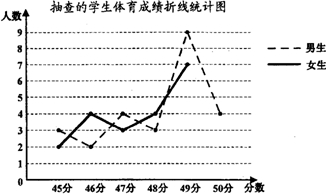
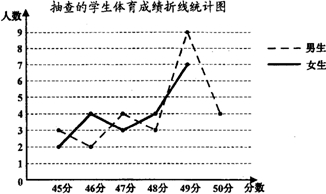
解:(1)抽查的学生人数为:(3+2)÷10%=50人;
由图可知,得分为45分的人数为:3+2=5,
得分为46分的人数为:2+4=6,
得分为47分的人数为:4+3=7,
得分为48分的人数为:3+4=7,
得分为49分的人数为:9+7=16,
所以,第25人的得分为48分,第26人的得分为49分,
中位数为
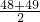
=48.5;
得分50分的女生人数为:50-5-6-7-7-16-4=50-45=5人.
所以,女生成绩的平均数为:
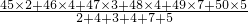
=
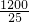
=48;
故答案为:50,48.5,48;
(2)女生得分50分的有5人,所以补全图形如图;

(3)设得分50分的男生分别为男1、男2、男3、男4,其中男1、男2是体育特长生,
得分50分的女生分别为女1、女2、女3、女4、女5,其中女1、女2是体育特长生,
列表如下:
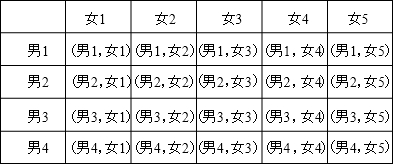
由表可知,一共有20种等可能情况,其中都不是体育特长生的有6种情况,
所以,P(都不是体育特长生)=
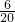
=

.
分析:(1)根据得分为45分的学生人数与所占的百分比列式计算即可求出被抽查的学生人数为50;根据中位数的定义找出第25、26两个人的得分,然后求平均数即可;先求出的50分的女生人数是5,再根据算术平均数的求法列式计算即可得解;
(2)根据得50分的女生人数为5,补全折线图即可;
(3)列出图表,然后根据概率公式列式计算即可得解.
点评:本题考查了折线统计图,中位数的定义,算术平均数的求解,用列表法求概率,列表法可以不重复不遗漏的列出所有可能的结果,用到的知识点为:概率=所求情况数与总情况数之比.

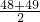 =48.5;
=48.5;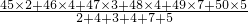 =
=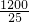 =48;
=48;

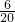 =
= .
.

 阅读快车系列答案
阅读快车系列答案