
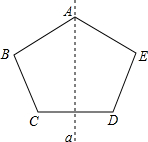
 如图,根据轴对称的性质可知:
如图,根据轴对称的性质可知: 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
 如图,根据轴对称的性质可知:
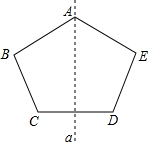
如图,根据轴对称的性质可知:查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2012届浙江省台州六校九年级上学期第二次联考数学卷(解析版) 题型:解答题
如图,△ABC中,∠BAC=90°,AC=2,AB= ,△ACD是等边三角形.
,△ACD是等边三角形.
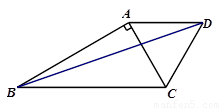
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,
画出旋转后的图形.
(3)求BD的长度.
【解析】(1)利用正切的知识可得出答案.
(2)根据旋转角度、旋转中心、旋转方向找出各点的对称点,顺次连接即可;
(3)根据旋转的性质可得△ACE≌△ADB,从而确定∠EBC=90°,然后利用勾股定理即可解答
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com