
【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
由线段![]() 所代表的意思,结合装货半小时,可得出
所代表的意思,结合装货半小时,可得出![]() 的值,从而判断出①成立;
的值,从而判断出①成立;
结合路程=速度×时间,能得出甲车的速度,从而判断出②成立;
设出乙车刚出发时的速度为![]() 千米/时,则装满货后的速度为
千米/时,则装满货后的速度为![]() 千米/时,由路程=速度×时间列出关于
千米/时,由路程=速度×时间列出关于![]() 的一元一次方程,解出方程即可得知乙车的初始速度,由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间,从而得出③成立;
的一元一次方程,解出方程即可得知乙车的初始速度,由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间,从而得出③成立;
由乙车刚到达货站的时间,可以得出甲车行驶的总路程,结合![]() 、
、![]() 两地的距离即可判断④也成立.
两地的距离即可判断④也成立.
综上可知①②③④皆成立.
![]() 线段
线段![]() 代表乙车在途中的货站装货耗时半小时,
代表乙车在途中的货站装货耗时半小时,
![]()
![]() (小时),即①成立;
(小时),即①成立;
![]() 分钟
分钟![]() 小时,
小时,
甲车的速度为![]() (千米/时),即②成立;
(千米/时),即②成立;
设乙车刚出发时的速度为![]() 千米/时,则装满货后的速度为
千米/时,则装满货后的速度为![]() 千米/时,
千米/时,
根据题意可知:![]() ,
,
解得:![]() ,
,
乙车发车时,甲车行驶的路程为![]() (千米),
(千米),
乙车追上甲车的时间为![]() (小时),
(小时),
![]() 小时
小时![]() 分钟,即③成立;
分钟,即③成立;
乙车刚到达货站时,甲车行驶的时间为![]() 小时,
小时,
此时甲车离![]() 地的距离为
地的距离为![]() (千米),即④成立;
(千米),即④成立;
综上可知正确的有:①②③④.
故选:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 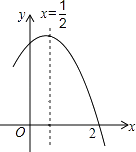
A.①②④
B.③④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形. 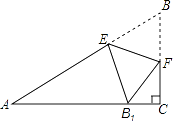
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张宽为1cm的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD, 
(1)试判断四边形ABCD的形状,并说明理由
(2)若∠BAD=30°,求重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金﹣各种费用)为275万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4. 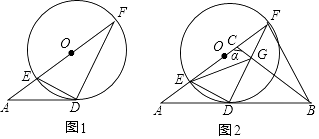
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y. ①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com