
分析 (1)设原计划每天铺设管道x米,根据等量关系:铺设120米管道的时间+铺设(300-120)米管道的时间=27天,可列方程求解.
(2)原计划所用天数-实际所用天数=少用的天数,即可得出结果.
解答 解:设原计划每天铺设管道x米,
依题意得:$\frac{120}{x}$+$\frac{300-120}{x(1+20%)}$=27,
解得:x=10,
经检验,x=10是原方程的解,且符合题意.
答:原计划每天铺设管道10米.
(2)∵$\frac{300}{10}$-27=3,
∴3×4000=12000(元),
答:现在比原计划少支出12000元钱.
点评 本题考查理解题意的能力,关键是设出原计划每天铺设管道x米,以天数做为等量关系列方程求解.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | -2013 | B. | 2013 | C. | $\frac{1}{2013}$ | D. | $-\frac{1}{2013}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
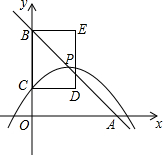 如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
如图,在平面直角坐标系中,直线y=-x+4与x轴、y轴分别交于点A、B.抛物线y=-$\frac{1}{3}{(x-m)^2}$+n的顶点P在直线y=-x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
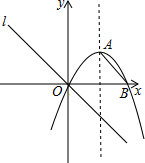 如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.
如图,抛物线y=ax2+2x与x轴交于点B,其对称轴为x=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
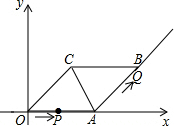 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
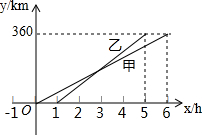 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com