
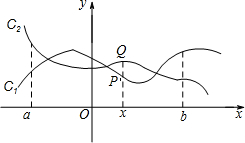
 如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.
如图,点P(x,y1))与Q(x,y2)分别是两个函数图象C1与C2上的任一点.当a≤x≤b时,有-1≤y1-y2≤1成立,则称这两个函数在a≤x≤b上是“相邻函数”,否则称它们在a≤x≤b上是“非相邻函数”.例如,点P(x,y1)与Q(x,y2)分别是两个函数y=3x+1与y=2x-1图象上的任一点,当-3≤x≤-1时,y1-y2=(3x+1)-(2x-1)=x+2,通过构造函数y=x+2并研究它在-3≤x≤-1上的性质,得到该函数值的范围是-1≤y≤1,所以-1≤y1-y2≤1成立,因此这两个函数在-3≤x≤-1上是“相邻函数”.分析 (1)判定函数y=3x+2与y=2x+1在-2≤x≤0上为“相邻函数”,利用给定的证明过程,将y1=3x+1、y2=2x-1替换成y1=3x+2、y2=2x+1即可得出结论;
(2)根据一次函数与反比例函数的单调性,分别找出当x=1、x=2时,y1、y2的值,再根据“相邻函数”的定义即可得出关于a的一元一次不等式组,解不等式组即可得出结论;
(3)将两函数解析式做差,找出y1-y2=(x-a)2+2-a2,结合二次函数的性质找出其最大值与最小值,再根据“相邻函数”的定义即可得出关于a的一元一次不等式组,解不等式组即可得出结论.
解答 解:(1)是“相邻函数”.
理由如下:
y1-y2=(3x+2)-(2x+1)=x+1,构造函数y=x+1.
∵y=x+1在-2≤x≤0上随着x的增大而增大,
∴当x=0时,函数有最大值1,当x=-2时,函数有最小值-1,即-1≤y≤1.
∴-1≤y1-y2≤1.
即函数y=3x+2与y=2x+1在-2≤x≤0上是“相邻函数”;
(2)反比例函数y=$\frac{2}{x}$在1≤x≤2上是减函数,
当x=1时,y1=2;当x=2时,y1=1,
当x=1时,y2=-2+a;当x=2时,y2=-4+a.
∵-1≤y1-y2≤1,
∴有$\left\{\begin{array}{l}{-1≤4-a≤1}\\{-1≤5-a≤1}\end{array}\right.$,
解得:4≤a≤5.
∴若函数y=$\frac{2}{x}$与y=-2x+a在1≤x≤2上是“相邻函数”,a的最大值为5,最小值为4;
(3)y1-y2=[x2-(2a-1)x]-(x-2)=x2-2ax+2=(x-a)2+2-a2.
∵y=x2-(2a-1)x与y=x-2在1≤x≤2上是“相邻函数”,
∴|y1-y2|≤1.
由二次函数的性质可知:
当x=1时,y1-y2有最大值3-2a,
当x=a时,y1-y2有最小值2-a2.
∴$\left\{\begin{array}{l}{-1≤3-2a≤1}\\{-1≤2-{a}^{2}≤1}\end{array}\right.$,
解得:$\frac{5}{4}$≤a≤$\sqrt{3}$.
点评 本题考查了一次函数的性质、反比例函数的性质以及二次函数的最值问题,解题的关键是:
(1)构造函数y=x+1,利用一次函数的性质解决问题;
(2)由“相邻函数”的性质得出关于a的一元一次不等式.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,结合给定的新定义,找出关于函数系数a的方程(不等式或不等式组)是关键.
(3)由“相邻函数”的性质得出关于a的一元一次不等式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{y}{x+y}$=$\frac{4}{7}$ | B. | $\frac{x}{x-y}$=3 | C. | $\frac{x+2y}{x}$=$\frac{10}{3}$ | D. | $\frac{x-y}{y}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
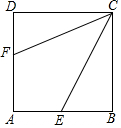 如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.
如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
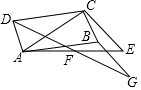 如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.
如图,已知四边形ABCD为平行四边形,线段CE垂直对角线AC,连接AE,点F为AE中点,连接DF并延长至点G,使FG=DF,连按BG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com