
����Ŀ���ס�������֮����һ����ֱ�Ĺ�·![]() ��С���Ӽس����ع�·
��С���Ӽس����ع�·![]() ����ǰ���ҵأ�ͬʱС�����ҵس����ع�·
����ǰ���ҵأ�ͬʱС�����ҵس����ع�·![]() �ﳵǰ���أ�С�������ͣ��һ��ʱ�䣬ԭ·ԭ�ٷ��أ���С��������һ���е��ҵ�.��С����صľ���Ϊ
�ﳵǰ���أ�С�������ͣ��һ��ʱ�䣬ԭ·ԭ�ٷ��أ���С��������һ���е��ҵ�.��С����صľ���Ϊ![]() (m)��С����صľ���Ϊ
(m)��С����صľ���Ϊ![]() (m)��С����С��֮��ľ���Ϊ
(m)��С����С��֮��ľ���Ϊ![]() (m)��С�����ߵ�ʱ��Ϊ
(m)��С�����ߵ�ʱ��Ϊ![]() (min).
(min).![]() ��
��![]() ��
��![]() ֮��ĺ���ͼ����ͼ�٣�
֮��ĺ���ͼ����ͼ�٣�![]() ��
��![]() ֮��ĺ���ͼ��(����)��ͼ��.
֮��ĺ���ͼ��(����)��ͼ��.
(1)��С�����ҵص��ع�����![]() (m)��
(m)��![]() (min)֮��ĺ�������ʽ;
(min)֮��ĺ�������ʽ;
(2)��С���Ӽط��ص���С�������Ĺ�����![]() (m)��
(m)��![]() ( min)֮��ĺ�������ʽ;
( min)֮��ĺ�������ʽ;
(3)��ͼ���У���ȫ����������![]() (m)��
(m)��![]() (min)֮��ĺ���ͼ��ȷ��
(min)֮��ĺ���ͼ��ȷ��![]() ��ֵ.
��ֵ.

���𰸡�(1) ![]() ��(2)
��(2) ![]() ��(3)
��(3)![]() ����ȫͼ�������.
����ȫͼ�������.
��������
(1)��С�����ҵص��ع�����y1���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x+b���ɴ���ϵ��������ͼ��Ϳ����������ʽ��
(2)�ȸ��ݺ���ͼ��������ҵ��ٶȣ�Ȼ����������Ϳ������С����С����ʱ�䣬�Ϳ������С���Ӽط��ص���С�������Ĺ�����s���ף���x�����ӣ�֮��ĺ�����ϵʽ��
(3)�ȸ����������⽨�����̾Ϳ������aֵ��10���Ӽס����ߵ�·�̾������ľ��룬14����С���ߵ�·�̺�С����С��ʱ��ʱ��Ϳ��Բ�����ͼ��.
(1)��С�����ҵص��ع�����y1���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x+b����ͼ�ã�![]() ����ã�
����ã�![]() ��
��
��y1=��240x+2400��
(2)�����⣬��С�����ٶ�Ϊ��2400��40=60��/�֣�С�����ٶ�Ϊ��2400��10=240��/�֣�
��С���Ӽ���С����ʱ��Ϊ24��60�£�240��60��=8���ӣ�
��24����ʱ���˵ľ���Ϊ��s=24��60=1440��32����ʱS=0��
��s��x֮��ĺ�����ϵʽΪ��s=kx+b1�������⣬��![]() ��
��
��ã�![]() ��
��
��s=��180x+5760��
(3)�����⣬��a=2400�£�240+60��=8���ӣ�
��x=24ʱ��s=1440����x=32ʱ��S=0��
�������Ӧ�ĵ�Ϳ��Բ�ȫͼ����ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���˿�����ȡ������3������6������10�������ƣ�ϴ�Ⱥ����泯�·��������ϣ�С����С����������Ϸ����Ϸ�������£�����С���������һ���ƣ������������ֺ�Żأ�ϴ�Ⱥ����泯�£�����С���������һ���ƣ������������֡�������Ϊһ����Ϸ���������������������ֲ�ͬʱ���������ִ�Ļ�ʤ������������������������ͬ����Ϊƽ�֣� 
��1���û���״ͼ���б������г�С����С������һ����Ϸ�����п��ܵĽ����
��2����С����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
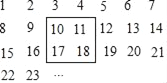
����Ŀ����������1��2��3��4�������г���ͼ��ʾ��һ������
��1����һ�������ڱ��������ס4��������������������Ϊx�����������ú�x��ʽ�ӱ�ʾ�������Ӵ�С�������� ������ ������ ����
��2���ڣ�1����ǰ���£�������ס��4����֮�͵���984ʱ��xλ�ڸñ��ĵڼ��еڼ��У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ��������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ���˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ������������
��1������ѡȡ�����ķ����������һ������ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ;
����ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ����ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ.
��2�����γ������鷢�֣����ܵ���ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�������ͼ��

����m��n��ֵ.
�ڲ�ȫ����ͳ��ͼ
�۸��ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
�ܼ�ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㡣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��1����Ϊ���˽�ͬѧ��һ���㻨Ǯ������������Ա���ͬѧ��չ�˵��飬��ͬѧһ�ܵ��㻨Ǯ��2ԪΪ��࣬������ͼ��Ƶ�ʷֲ�ֱ��ͼ����֪�����Ҹ����Ƶ��֮��Ϊ2��3��4��2��1.

��1�����ð���48�ˣ����㻨Ǯ�������ǵ�_____�飬��_______�ˣ�
��2���㻨Ǯ��8Ԫ���ϵĹ���_____�ˣ�
��3����ÿ���ƽ�����Ѱ����ֵ���㣬��ð�ͬѧ����ƽ�����Ѷ���_______Ԫ����ȷ��0.1Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ͳ�ƾַ�����ͳ��������ʾ�������н�5�����������ֵ������ͼ1��ʾ��2016�����������ֵ�е�һ��ҵ���ڶ���ҵ��������ҵ��ռ������ͼ2��ʾ��
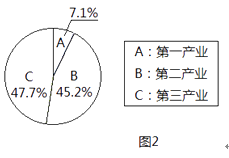
�����ͼ����Ϣ������������⣺
��1����2016���һ��ҵ������ֵ����ȷ��1��Ԫ����
��2��2016���2015��Ĺ���������ֵ�����˰ٷ�֮������ȷ��1%����
��3����Ҫʹ2018��Ĺ���������ֵ�ﵽ1573��Ԫ����2016����2018�����й���������ֵƽ���������ʣ���ȷ��1%����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����
С����������һ�����⣺�����![]() ���ö���ʽ��һ����ϵ����
���ö���ʽ��һ����ϵ����
С����ͨ������![]() ���õĶ���ʽ�����������⣬���о���Щ����������̽Ѱһ�£��Ƿ�����Լ��ķ�����
���õĶ���ʽ�����������⣬���о���Щ����������̽Ѱһ�£��Ƿ�����Լ��ķ�����
�������Ӽ������ʼ������![]() ���ö���ʽ�е�һ����ϵ����ͨ���۲췢�֣�
���ö���ʽ�е�һ����ϵ����ͨ���۲췢�֣�
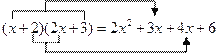
Ҳ����˵��ֻ����![]() �е�һ����ϵ��1����
�е�һ����ϵ��1����![]() �еij�����3������
�еij�����3������![]() �еij�����2����
�еij�����2����![]() �е�һ����ϵ��2�����������
�е�һ����ϵ��2�����������![]() �����ɵõ�һ����ϵ����
�����ɵõ�һ����ϵ����
��������ķ����������![]() ���ö���ʽ��һ����ϵ������������
���ö���ʽ��һ����ϵ������������![]() ��һ����ϵ��1��
��һ����ϵ��1�� ![]() �ij�����3��
�ij�����3�� ![]() �ij�����4����˵õ�12������
�ij�����4����˵õ�12������![]() ��һ����ϵ��2��
��һ����ϵ��2�� ![]() �ij�����2��
�ij�����2�� ![]() �ij�����4����˵õ�16��Ȼ����
�ij�����4����˵õ�16��Ȼ����![]() ��һ����ϵ��3��
��һ����ϵ��3�� ![]() �ij�����2��
�ij�����2�� ![]() �ij�����3����˵õ�18�����12��16��18��ӣ��õ���һ����ϵ��Ϊ46��
�ij�����3����˵õ�18�����12��16��18��ӣ��õ���һ����ϵ��Ϊ46��
�ο�С��˼������ķ���������������⣺
��1������![]() ���ö���ʽ��һ����ϵ��Ϊ ��
���ö���ʽ��һ����ϵ��Ϊ ��
��2������![]() ���ö���ʽ��һ����ϵ��Ϊ ��
���ö���ʽ��һ����ϵ��Ϊ ��
��3��������![]() ���ö���ʽ��һ����ϵ��Ϊ0����
���ö���ʽ��һ����ϵ��Ϊ0����![]() =_________��
=_________��
��4����![]() ��
��![]() ��һ����ʽ����
��һ����ʽ����![]() ��ֵΪ ��
��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���и����ȵ���ʮ����������ӣ�����1���������1����2���������2����3���������3����2���������4����1���������5���������������6�������������������
(1)������6�����ϵĿ������ж��
(2)��Щ���ֳ��ϵĿ�����һ����
(3)��Щ���ֳ��ϵĿ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB
��1�����ó߹水����Ҫ����ͼ��
���ӳ��߶�AB��C��ʹBC��AB��
���ӳ��߶�BA��D��ʹAD��AC����д��������Ҫ������ͼ�ۼ���
��2����ֱ�ӻش��߶�BD���߶�AC����֮��Ĵ�С��ϵ
��3�����AB��2cm��������߶�BD��CD�ij��ȣ�
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com