
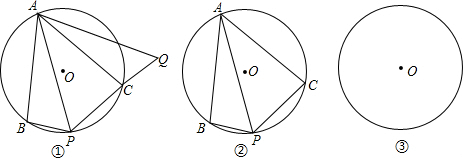
分析 (1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;
(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;
(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.
解答 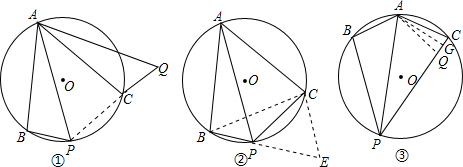 (1)证明:如图①,连接PC.
(1)证明:如图①,连接PC.
∵△ACQ是由△ABP绕点A逆时针旋转得到的,
∴∠ABP=∠ACQ.
由图①知,点A、B、P、C四点共圆,
∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),
∴∠ACP+∠ACQ=180°(等量代换);
(2)解:PA=PB+PC.理由如下:
如图②,连接BC,延长BP至E,使PE=PC,连接CE.
∵弦AB=弦AC,∠BAC=60°,
∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠ECP=∠EPC=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP(等量代换).
在△BEC和△APC中,$\left\{\begin{array}{l}{CE=PC}\\{∠BCE=∠ACP}\\{AC=BC}\end{array}\right.$,
∴△BEC≌△APC(SAS),
∴BE=PA,
∴PA=BE=PB+PC;
(3)若∠BAC=120°时,(2)中的结论不成立.$\sqrt{3}$PA=PB+PC.理由如下:
如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.
∵∠BAC=120°,∠BAC+∠BPC=180°,
∴∠BPC=60°.
∵弦AB=弦AC,
∴∠APB=∠APQ=30°.
在△ABP和△AQP中,
∵$\left\{\begin{array}{l}{PB=PQ}\\{∠APB=∠APQ}\\{AP=AP}\end{array}\right.$,
∴△ABP≌△AQP(SAS),
∴AB=AQ,PB=PQ(全等三角形的对应边相等),
∴AQ=AC(等量代换).
在等腰△AQC中,QG=CG.
在Rt△APG中,∠APG=30°,则AP=2AG,PG=$\sqrt{3}$AG.
∴PB+PC=PG-QG+PG+CG=PG-QG+PG+QG=2PG=2$\sqrt{3}$AG,
∴$\sqrt{3}$PA=2$\sqrt{3}$AG,即$\sqrt{3}$PA=PB+PC.
点评 本题考查了圆心角、弧、弦间的关系,等腰三角形的性质,全等三角形的判定与性质,等边三角形的判定和性质,四点共圆,圆内接四边形的性质,正确的作出辅助线是解题的关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:解答题
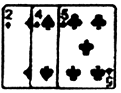 三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.
三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
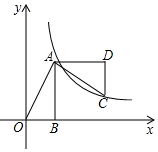 如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )
如图,已知在Rt△AOB中,点A(1,2),∠OBA=90°,OB在x轴上,将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(k>0)上,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
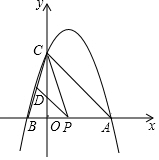 如图,已知二次函数y=ax2+bx+4的图象经过点A(4,0)、B(-2,0).
如图,已知二次函数y=ax2+bx+4的图象经过点A(4,0)、B(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com