
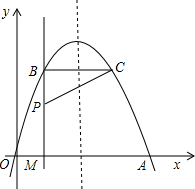
 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.分析 (1)把m=3代入得到抛物线的解析式,然后令y=0得:-x(x-6)=0,从而可求得点A的坐标,利用抛物线的对称性可得到抛物线的对称轴为x=m,然后利用抛物线的对称性可得到BC的长;
(2)过点C作AH⊥x轴,垂足为H.先求得点B和点C的坐标,由点B、点P和点C的坐标可得到PB、BC的长,然后由点C和点A的坐标可求得CH,AH的长,接下来,再证明△ACH∽△PCB,最后依据相似三角形的性质列方程求解即可;
(3)当m>1时,BC=2(m-1),PM=m,BP=m-1.①若点E在x轴上时,先证明△BPC≌△MEP,依据全等三角形的性质可得到BC=PM,然后依据BC=PM可得到关于m的方程,从而可求得m的值,故此可得到E的坐标;②若点E在y轴上,过点P作PN⊥y轴与点N.然后证明△BPC≌△NPE,则BP=NP=OM=1,则m-1=1,可求得m=2,于是可求得点E的坐标.
解答 解:(1)当m=3时,y=-x2+6x=-x(x-6).
令y=0得:-x(x-6)=0,解得x=0或x=6,
∴点A的坐标为(6,0).
∴抛物线的对称轴为直线x=3.
∵B、C关于直线x=3对称,
∴BC=2×(3-1)=4.
(2)如图1所示:过点C作AH⊥x轴,垂足为H.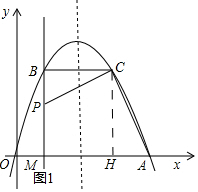
∵抛物线y=-x2+2mx的对称轴为x=m,
∴点B和点C直线x=m对称.
∵当x=1时,y=2m-1,
∴点B的坐标为(1,2m-1).
∴PB=m-1.
∵点B与点C关于直线x=m对称,
∴C(2m-1,2m-1).
∴BC=2m-2.
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∵∠ACH=∠PCB=90°,
∴∠ACH=∠BCP.
又∵∠AHC=∠PCB=90°,
∴△ACH∽△PCB.
∴$\frac{AH}{CH}$=$\frac{PB}{BC}$,即$\frac{1}{2m-1}$=$\frac{m-1}{2(m-1)}$,
∴m=$\frac{3}{2}$.
(3)当m>1时,BC=2(m-1),PM=m,BP=m-1.
①若点E在x轴上时,如图2所示: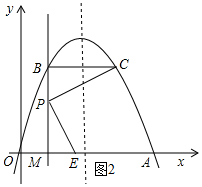
∵∠CPE=90°,
∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP.
在△BPC和△MEP中,$\left\{\begin{array}{l}{∠PBC=∠PME=90°}\\{∠BPC=∠MEP}\\{PC=EP}\end{array}\right.$,
∴△BPC≌△MEP.
∴BC=PM.
∴2(m-1)=m,解得m=2,
∴E(2,0).
若点E在y轴上,如图3所示:过点P作PN⊥y轴与点N.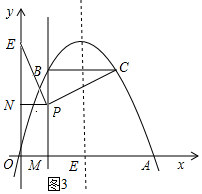
∵∠EPC=90°,
∴∠EPB+∠BPC=90°.
∵∠NPE+∠EPB=90°,∠NEP=∠EPB,
∴∠BPC=∠EPN.
在△EPN和△CPB中,$\left\{\begin{array}{l}{∠BPC=∠EPN}\\{∠PNE=∠PBC=90°}\\{PE=PC}\end{array}\right.$
∴△BPC≌△NPE.
∴BP=NP=OM=1,
∴m-1=1,
∴m=2
∴E(0,4).
综上所述,当m=2时,点E的坐标为(2,0)或(0,4).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的判定和性质、全等三角形的性质和判定,依据全等三角形的性质得到相关线段的长度相等,从而列出关于m的方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
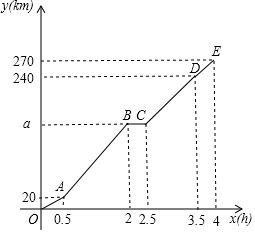 小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.
小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
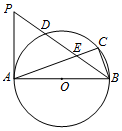 如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
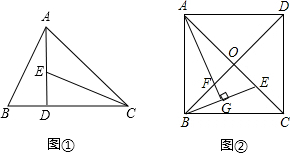
 如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.
如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
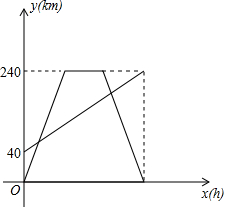 A,B两地相距240km,甲骑摩托车由A地驶往B地,出发1小时后,乙驾驶汽车由B地驶往A地,乙达到A地停留1小时后,按原路原速返回B地,恰好与甲同时到达B地,乙行驶过程中两人均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
A,B两地相距240km,甲骑摩托车由A地驶往B地,出发1小时后,乙驾驶汽车由B地驶往A地,乙达到A地停留1小时后,按原路原速返回B地,恰好与甲同时到达B地,乙行驶过程中两人均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com