
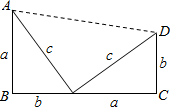
 利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为________,该定理的结论其数学表达式是________.
利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为________,该定理的结论其数学表达式是________.科目:初中数学 来源: 题型:044
(2006,济南)某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图(1),废纸箱的一面利用墙,放置在地面上,利用地面作底,其他的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.
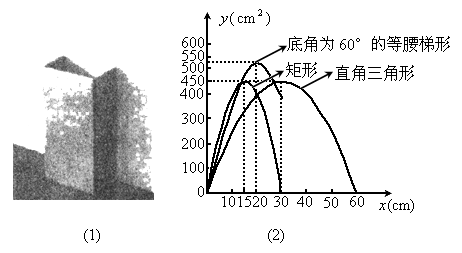
(1)该小组通过多次尝试,最终选定下表中的简便且易操作的三种横截面图形,如图(2),是根据这三种横截面图形的面积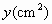 与x(cm)(见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有关信息,在表中空白处填上适当的数、式,并完成y取最大值时的设计示意图;
与x(cm)(见表中横截面图形所示)的函数关系式而绘制出的图象.请你根据有关信息,在表中空白处填上适当的数、式,并完成y取最大值时的设计示意图;
 (2)在研究性学习小组展示研究成果时,小华同学指出:图(2)中“底角为60°的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
(2)在研究性学习小组展示研究成果时,小华同学指出:图(2)中“底角为60°的等腰梯形”的图象与其他两个图象比较,还缺少一部分,应该补画.你认为他的说法正确吗?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com