
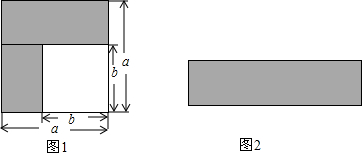
分析 (1)利用正方形的面积公式,图①阴影部分的面积为大正方形的面积-小正方形的面积,图②长方形的长为a+b,宽为a-b,利用长方形的面积公式可得结论;
(2)由(1)建立等量关系即可;
(3)根据平方差公式即可解答.
解答 解:(1)图①阴影部分的面积为:a2-b2,图②长方形的长为a+b,宽为a-b,所以面积为:(a+b)(a-b),
故答案为:a2-b2,(a+b)(a-b);
(2)由(1)可得:(a+b)(a-b)=a2-b2,
故答案为:(a+b)(a-b)=a2-b2;
(3)20162-2017×2015.
=20162-(2016+1)(2016-1)
=20162-20162+1
=1.
点评 本题主要考查了平方差公式的推导过程,利用面积建立等量关系是解答此题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条线段可以组成一个三角形 | |
| B. | 打开电视机正在播放动画片 | |
| C. | 车辆随机经过一个路口,遇到绿灯 | |
| D. | 掷一枚均匀的骰子,掷出的点数是奇数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚骰子,点数为3的一面朝上 | |
| B. | 在一副扑克牌中随意抽7张牌,其中有4张是Q | |
| C. | 从1、3、5、7四个数中,随意取两个数,这两个数之和为偶数 | |
| D. | 同时掷两枚骰子,这两枚骰子的点数相乘的积为40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com