(1)x2+4x-5=0(配方法)
(2)3x2+7x+4=0(公式法)
解:(1)x
2+4x-5=0,
移项得:x
2+4x=5,
两边都加上4,变形得:(x+2)
2=9,
可得:x+2=3或x+2=-3,
∴x
1=1,x
2=-5
(2)3x
2+7x+4=0,
∵a=3,b=7,c=4,
∴b
2-4ac=49-48=1>0,
∴x=
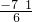
,
∴x
1=-1,x
2=-

.
分析:(1)将常数项-5变号后移项到方程右边,然后方程两边都加上一次项系数一半的平方4,左边利用完全平方公式变形,右边合并,开方后转化为两个一元一次方程,求出方程的解即可得到原方程的解;
(2)找出原方程的二次项系数a,一次项系数b及常数项c,计算出b
2-4ac的值,发现其值大于0,然后利用求根公式即可求出原方程的解.
点评:此题考查了利用配方法及公式法求一元二次方程的解,配方法解方程时,应先将二次项系数化为1,然后将常数项移项到方程右边,两边都加上一次项系数一半的平方,变形开方后转化为两个一元一次方程来求解;公式法求解方程时,应先将方程化为一般形式,找出a,b及c的值,计算出根的判别式b
2-4ac的值,当根的判别式b
2-4ac≥0时,代入求根公式即可求出方程的解.

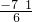 ,
, .
.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案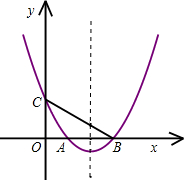 与原抛物线交于点M,当△MA′B′的面积为
与原抛物线交于点M,当△MA′B′的面积为