
 直线
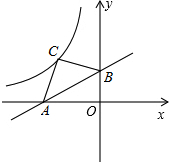
直线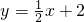 与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,
与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,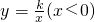 的图象过点C,则k=________.
的图象过点C,则k=________. ,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB=
,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB= AB=
AB= ,
, CA•CB+
CA•CB+ OA•OB=9,则CD=CE=3,可确定C点坐标为(-3,3),然后把C点坐标代入反比例函数解析式即可得到k的值.
OA•OB=9,则CD=CE=3,可确定C点坐标为(-3,3),然后把C点坐标代入反比例函数解析式即可得到k的值.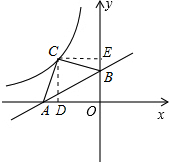 过C点作CD⊥x轴于D,CE⊥y轴于E,
过C点作CD⊥x轴于D,CE⊥y轴于E, x+2=0,解得x=-4,则A点坐标为(-4,0),B点坐标为(0,2),
x+2=0,解得x=-4,则A点坐标为(-4,0),B点坐标为(0,2), =2
=2 ,
, AB=
AB= ,
, CA•CB+
CA•CB+ OA•OB=
OA•OB=
 ×
× +
+ ×4×2=9,
×4×2=9, 得k=-3×3=-9.
得k=-3×3=-9.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
| A、9个 | B、7个 | C、5个 | D、3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省武汉市盘龙一中九年级(上)期中数学试卷(解析版) 题型:填空题
 与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC,
与两坐标轴交于A、B两点,以AB为斜边在第二象限内作等腰Rt△ABC, 的图象过点C,则k= .
的图象过点C,则k= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com