Question

【题目】如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.

（1）依题意补全图形；（2）若∠PAC＝20°，求∠AEB的度数；

（3）连结CE，写出AE, BE, CE之间的数量关系，并证明你的结论．

Answer 1

【答案】（1）见解析；（2）60°；（3）CE ＋AE＝BE，理由见解析

【解析】试题分析：（1）根据题意补全图形即可；（2）根据轴对称的性质可得AC＝AD，∠PAC＝∠PAD=20°，根据等边三角形的性质可得AC＝AB，∠BAC＝60°，即可得AB＝AD，在△ABD 中，根据等腰三角形的性质和三角形的内角和定理求得∠D的度数，再由三角形外角的性质即可求得∠AEB的度数；（3）CE ＋AE＝BE，如图，在BE上取点M使ME＝AE，连接AM，设∠EAC＝∠DAE＝x，类比（2）的方法求得∠AEB＝60°，从而得到△AME为等边三角形，根据等边三角形的性质和SAS即可判定△AEC≌△AMB，根据全等三角形的性质可得CE＝BM，由此即可证得CE ＋AE＝BE．

试题解析：

(1)如图：

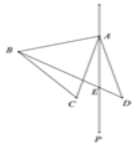
（2）在等边△ABC中，

AC＝AB，∠BAC＝60°

由对称可知：AC＝AD，∠PAC＝∠PAD，

∴AB＝AD

∴∠ABD＝∠D

∵∠PAC＝20°

∴∠PAD＝20°

∴∠BAD＝∠BAC+∠PAC +∠PAD =100°

.

∴∠AEB＝∠D+∠PAD＝60°

（3）CE ＋AE＝BE．

在BE上取点M使ME＝AE，连接AM，

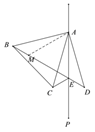
在等边△ABC中，

AC＝AB，∠BAC＝60°

由对称可知：AC＝AD，∠EAC＝∠EAD，

设∠EAC＝∠DAE＝x．

∵AD ＝AC＝AB，

∴

∴∠AEB＝60－x＋x ＝60°．

∴△AME为等边三角形．

∴AM=AE，∠MAE=60°，

∴∠BAC=∠MAE=60°，

即可得∠BAM=∠CAE.

在△AMB和△AEC中，

，

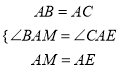∴△AMB≌△AEC.

∴CE＝BM.

∴CE ＋AE＝BE．