科目：初中数学 来源：山东省青岛市2018届九年级(北师大版)上期中数学检测试卷（1-4章） 题型：单选题
正方形具有而菱形不一定具有的性质是（ ）
A. 对角线互相平分 B. 对角线相等
C. 对角线互相垂直 D. 对角线平分对角
查看答案和解析>>
科目：初中数学 来源：2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型：解答题
勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给
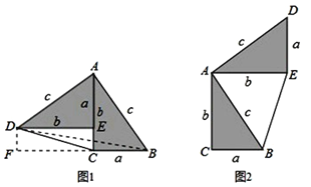
了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2 ．
证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=
b2+ab.
又∵S四边形ADCB=S△ADB+ S△DCB=c2+a(b-a).
∴b2+ab=c2+a(b-a)
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明．
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2．
查看答案和解析>>
科目：初中数学 来源：2018-2019学年度北师大版数学八年级上册 第1章《勾股定理》单元测试卷 题型：单选题
如图，CD是一平面镜，光线从A点射出经CD上的E点反射后照射到B点，设入射角为α（入射角等于反射角），AC⊥CD，BD⊥CD，垂足分别为C、D，且AC＝3，BD＝6，CD＝12，则CE的值为（ ）
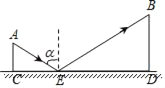
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源：浙江省湖州市2017-2018学年八年级上期期中考试数学试卷 题型：解答题
在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E.
(1)如图1，连接EC，求证：△EBC是等边三角形；
(2)点M是线段CD上的一点(不与点C，D重合)，以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G.求证：AD=DG+MD；
(3)点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G.请在图3中画出图形，并直接写出ND，DG与AD数量之间的关系.
查看答案和解析>>
科目：初中数学 来源：云南省2017-2018学年七年级上学期期中考试数学试卷 题型：填空题
若a、b互为相反数，c、d互为倒数，m的绝对值为2，则：
+3cd+m的值为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
｜＝________.
B. 
C. 
D. 