
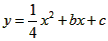 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1。
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1。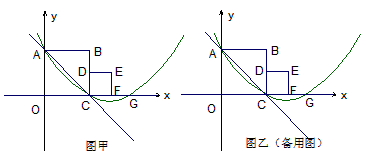
| 解:(1)如图甲,连接PE、PB,设PC=n, ∵正方形CDEF面积为1, ∴CD=CF=1, 根据圆和正方形的对称性知OP=PC=n, ∴BC=2PC=2n, 而PB=PE, 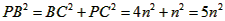 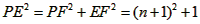 ∴ 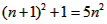 , ,解得n=1( 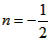 舍去), 舍去),∴BC=OC=2, ∴B点坐标为(2,2); |
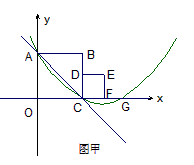 |
| (2)如图甲,由(1)知A(0,2),C(2,0), ∵A,C在抛物线上, ∴ 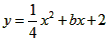 , ,∴ 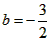 , ,∴抛物线的解析式为 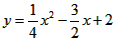 , ,即 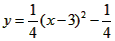 , ,∴抛物线的对称轴为x=3,即EF所在直线, ∵C与G关于直线x=3对称, ∴CF=FG=1, ∴FM= 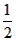 FG= FG=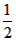 , ,在Rt△PEF与Rt△EMF中, 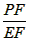 =2, =2,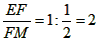 ∴ 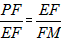 , ,∴△PEF∽△EMF, ∴∠EPF=∠FEM, ∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°, ∴ME与⊙P相切; |
|
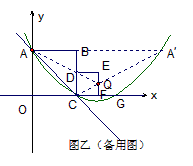
| (3)①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ则有AQ=A′Q, △ACQ周长的最小值为(AC+A′C)的长, ∵A与A′关于直线x=3对称∴A(0,2),A′(6,2), ∴ 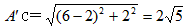 (6-2), (6-2),而AC= 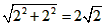 , ,∴△ACQ周长的最小值为 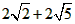 ; ;②当Q点在F点上方时,S=t+1, 当Q点在线段FN上时,S=1-t, 当Q点在N点下方时,S=t-1。 |
 |


科目:初中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源:2012届江苏省江阴市长泾片九年级下学期期中检测数学试卷(带解析) 题型:解答题
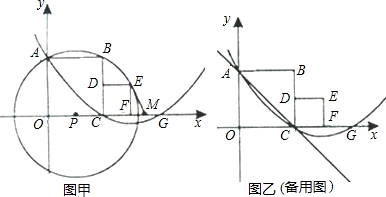
如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为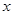 轴、
轴、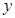 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在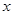 轴上),抛物线
轴上),抛物线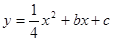 经过A、C两点,与
经过A、C两点,与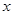 轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
【小题1】求B点坐标;
【小题2】求证:ME是⊙P的切线;
【小题3】设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;②若FQ=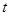 ,△ACQ的面积 S△ACQ=
,△ACQ的面积 S△ACQ=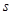 ,直接写出
,直接写出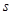 与
与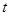 之间的函数关系式.
之间的函数关系式.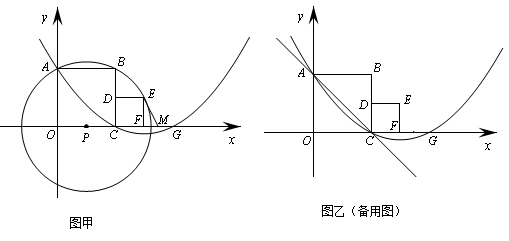
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省无锡市江阴市澄东片九年级(下)期中数学试卷(解析版) 题型:解答题
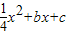 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.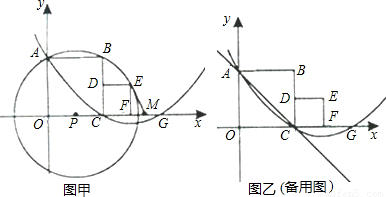
查看答案和解析>>
科目:初中数学 来源:2012年江苏省无锡市江阴市中考数学模拟试卷(4月份)(解析版) 题型:解答题
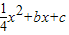 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.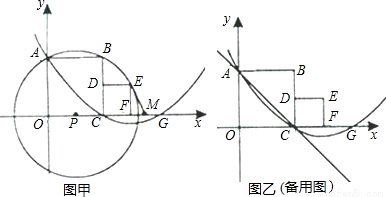
查看答案和解析>>
科目:初中数学 来源:2011年湖北省荆州市中考数学试卷(解析版) 题型:解答题
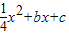 经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.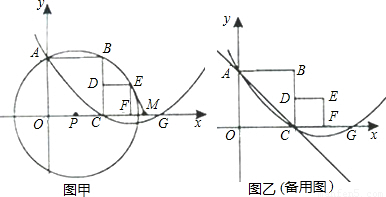
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com