
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)P的坐标 ,C的坐标 ;
(2)直线1上是否存在点Q,使△PBQ的面积等于△PAC面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.

【答案】(1)(3,4),(0,﹣5);(2)存在,点Q的坐标为:(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣5)
,﹣5)
【解析】
(1)利用配方法求出顶点坐标,令x=0,可得y=-5,推出C(0,-5);
(2)直线PC的解析式为y=3x-5,设直线交x轴于D,则D(![]() ,0),设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,分两种情形分别求解即可解决问题.
,0),设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,分两种情形分别求解即可解决问题.
解:(1)∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴顶点P(3,4),
令x=0得到y=﹣5,
∴C(0,﹣5).
故答案为:(3,4),(0,﹣5);
(2)令y=0,x2﹣6x+5=0,
解得:x=1或x=5,
∴A(1,0),B(5,0),
设直线PC的解析式为y=kx+b,则有![]() ,
,
解得:![]() ,
,
∴直线PC的解析式为:y=3x﹣5,
设直线交x轴于D,则D(![]() ,0),
,0),
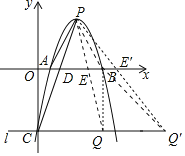
设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,
∵AD=![]() ,
,
∴BE=![]() ,
,
∴E(![]() ,0)或E′(
,0)或E′(![]() ,0),
,0),
则直线PE的解析式为:y=﹣6x+22,
∴Q(![]() ,﹣5),
,﹣5),
直线PE′的解析式为y=﹣![]() x+
x+![]() ,
,
∴Q′(![]() ,﹣5),
,﹣5),
综上所述,满足条件的点Q的坐标为:(![]() ,﹣5)或(
,﹣5)或(![]() ,﹣5);
,﹣5);


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知点P为抛物线y![]() x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
x2上一动点,以P为顶点,且经过原点O的抛物线,记作“yp”,设其与x轴另一交点为A,点P的横坐标为m.
(1)①当△OPA为直角三角形时,m= ;
②当△OPA为等边三角形时,求此时“yp”的解析式;
(2)若P点的横坐标分别为1,2,3,…n(n为正整数)时,抛物线“yp”分别记作“![]() ”、“
”、“![]() ”…,“
”…,“![]() ”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
”,设其与x轴另外一交点分别为A1,A2,A3,…An,过P1,P2,P3,…Pn作x轴的垂线,垂足分别为H1,H2,H3,…Hn.
1)① Pn的坐标为 ;OAn= ;(用含n的代数式来表示)
②当PnHn﹣OAn=16时,求n的值.
2)是否存在这样的An,使得∠OP4An=90°,若存在,求n的值;若不存在,请说明理由.
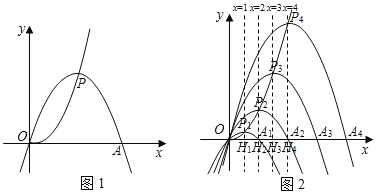
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠C=90°,按以下步骤作图:
①以点A为圆心,以小于AC的长为半径作弧,分别交AC、AB于点M,N;
②分别以点M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点O;
MN的长为半径作弧,两弧相交于点O;
③作射线OA,交BC于点E,若CE=6,BE=10.
则AB的长为( )
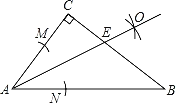
A.11B.12C.18D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知C点坐标为(0,4),抛物线的顶点的横坐标为
与x轴交于A、B两点,与y轴交于点C,已知C点坐标为(0,4),抛物线的顶点的横坐标为![]() ,点P是第四象限内抛物线上的动点,四边形OPAQ是平行四边形,设点P的横坐标为m.
,点P是第四象限内抛物线上的动点,四边形OPAQ是平行四边形,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求使△APC的面积为整数的P点的个数;
(3)当点P在抛物线上运动时,四边形OPAQ可能是正方形吗?若可能,请求出点P的坐标,若不可能,请说明理由;
(4)在点Q随点P运动的过程中,当点Q恰好落在直线AC上时,则称点Q为“和谐点”,如图(2)所示,请直接写出当Q为“和谐点”的横坐标的值.
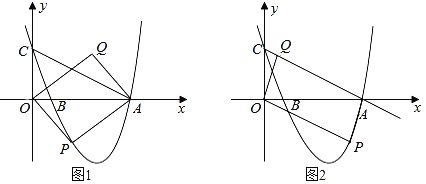
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点![]() .甲从中山路上点
.甲从中山路上点![]() 出发,骑车向北匀速直行;与此同时,乙从点
出发,骑车向北匀速直行;与此同时,乙从点![]() 出发,沿北京路步行向东匀速直行.设出发
出发,沿北京路步行向东匀速直行.设出发![]() 时,甲、乙两人与点
时,甲、乙两人与点![]() 的距离分别为
的距离分别为![]() 、
、![]() .已知
.已知![]() 、
、![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
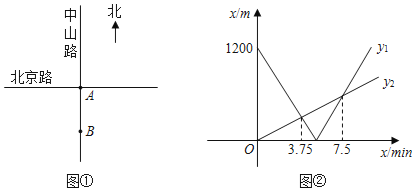
(1)求甲、乙两人的速度;
(2)当![]() 取何值时,甲、乙两人之间的距离最短?
取何值时,甲、乙两人之间的距离最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点F是⊙O上一点,且![]() =
=![]() ,连接FB,FD,FD交AB于点N.
,连接FB,FD,FD交AB于点N.
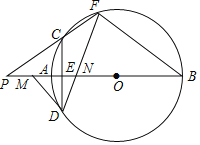
(1)若AE=1,CD=6,求⊙O的半径;
(2)求证:△BNF为等腰三角形;
(3)连接FC并延长,交BA的延长线于点P,过点D作⊙O的切线,交BA的延长线于点M.求证:ONOP=OEOM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
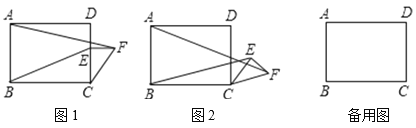
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线L:y=ax2+bx+c经过点A(-3,0)、B(0,4)和F(4,0).
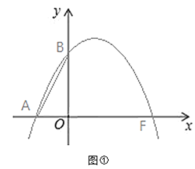
(1)求抛物线L的解析式;
(2)在图①抛物线L上,求作点C(保留作图痕迹,不写作法),使∠BAC=∠FAC,并求出点C的坐标;
(3)在图①中,若点D为抛物线上一动点,过点D作DH⊥x轴于点H,交直线AC于点G,过点C作CK⊥x轴于点K,连接DC,当以点G,C,D为顶点的三角形与△ACK相似时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com