Question

已知抛物线y=ax²+bx+c的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，3），过点C作x轴的平行线与抛物线交于点D，抛物线的顶点为M，直线y=x+5经过D、M两点．
（1）求此抛物线的解析式；
（2）连接AM、AC、BC，试比较∠MAB和∠ACB的大小，并说明你的理由．

Answer 1

分析：（1）由于CD∥x轴，将C点纵坐标代入直线DM的解析式中，即可得到D点的坐标，进而可得到抛物线的对称轴方程，再根据直线DM的解析式，即可求得抛物线的顶点坐标，进而可利用待定系数法求得该抛物线的解析式．
（2）根据抛物线的解析式，可求得A、B两点坐标，即可得到OA=OC=3，故△OAC是等腰直角三角形，若过B作BP⊥AC于P，则△ABP也是等腰直角三角形，即可得到AP、BP的长，进而可求得CP的值，从而在Rt△BCP中求得∠BPC的正切值；同理，可过M作x轴的垂线，根据M点的坐标，即可得到∠MAB的正切值，然后比较这两个角的正切值即可得到两个角的大小关系．

解答：解：（1）∵CD∥x轴且点C（0，3），
∴设点D的坐标为（x，3），
∵直线y=x+5经过D点，
∴3=x+5，
∴x=-2，
即点D（-2，3），
根据抛物线的对称性，设顶点的坐标为M（-1，y），
又∵直线y=x+5经过M点，
∴y=-1+5，y=4、即M（-1，4），
∴设抛物线的解析式为y=a（x+1）²+4，
∵点C（0，3）在抛物线上，
∴a=-1，
即抛物线的解析式为y=-x²-2x+3．（3分）


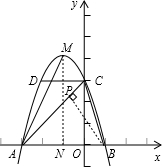
（2）作BP⊥AC于点P，MN⊥AB于点N；
由（1）中抛物线y=-x²-2x+3可得：
点A（-3，0），B（1，0），
∴AB=4，AO=CO=3，AC=3

2

，
∴∠PAB=45°；
∵∠ABP=45°，
∴PA=PB=2

2

，
∴PC=AC-PA=

2

；
在Rt△BPC中，tan∠BCP=

PB

PC

=2，
在Rt△ANM中，∵M（-1，4），
∴MN=4
、∴AN=2，
tan∠NAM=

MN

AN

=2，
∴∠BCP=∠NAM，
即∠ACB=∠MAB．（8分）

点评：此题主要考查了二次函数解析式的确定以及解直角三角形的应用，难度适中．