
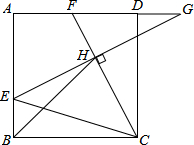
 如图,在边长为6
如图,在边长为6| 2 |
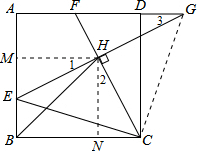 解:如图所示,连接CG.
解:如图所示,连接CG.
|
|
| 2 |
| 2 |
| 2 |
| 2 |
| 10 |
| 10 |
| CH |
| FG |
| HN |
| GH |
2
| ||
| FG |
4
| ||
2
|
| 2 |
| 2 |


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
 在平面直角坐标系xOy中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作lPBM.
在平面直角坐标系xOy中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作lPBM.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-
如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=-| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
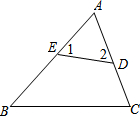 如图,BE=CF中,AF=DE,△ABF≌△DCE两点分别在边ABCD上,且DE与BC不平行.请填上一个你认为合适的条件:
如图,BE=CF中,AF=DE,△ABF≌△DCE两点分别在边ABCD上,且DE与BC不平行.请填上一个你认为合适的条件:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com