练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，多边形ABCDEF是正六边形，六个顶点中纵坐标相同的点有
    3
    3
    对；关于x轴对称的点有
    2
    2
    对，到原点距离相等的点有
    6
    6
    个．
    分析：根据正六边形的性质以及关于x轴对称和点的坐标性质分别得出即可．
    解答：解：根据图形中点的坐标特点得出：六个顶点中纵坐标相同的点有：E和F，B和C，A和D一共有3对；
    关于x轴对称的点有E和C，F和B，一共有2对，
    到原点距离相等的点有A，B，C，D，E，F都到原点距离相等，故一共有6个．
    故答案为：3，2，6．
    点评：此题主要考查了坐标与图形的性质，根据坐标系中点的坐标性质得出是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．
    （1）求该抛物线所对应的函数关系式；
    （2）将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．
    ①当t=
    52
    时，判断点P是否在直线ME上，并说明理由；
    ②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    25、已知：如图所示，△ABC中，E、F、D分别是AB、AC、BC上的点，且DE∥AC，DF∥AB，要使四边形AEDF是菱形，在不改变图形的前提下，你需添加的一个条件是
    AE=AF
    ，试证明：这个多边形是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•江西模拟）在等腰三角形ABC中，AB=AC，∠B=30°，若将若干个这样的三角形按如图所示的方式拼接在一起，使每个等腰三角形的顶角的顶点与前一个三角形的底角顶点重合，一腰在前一个等腰三角形的底边上，直至最后一个三角形的底角顶点与点A重合，则这样拼成的多边形的形状为
    正十二边形
    正十二边形
    ．

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年福建省莆田市仙游县第二教研片区九年级（上）期末联考数学试卷（解析版） 题型：解答题

    如图，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．
    （1）求该抛物线所对应的函数关系式；
    （2）将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．
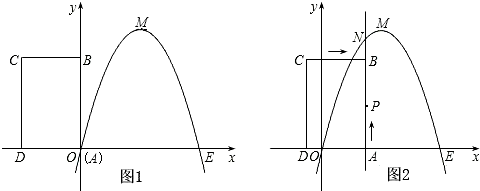
    ①当t=时，判断点P是否在直线ME上，并说明理由；
    ②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2011年河南省平顶山市中考数学二模试卷（解析版） 题型：解答题

    如图，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．
    （1）求该抛物线所对应的函数关系式；
    （2）将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．
    ①当t=时，判断点P是否在直线ME上，并说明理由；
    ②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案