
 如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π.
如图,已知长方形ABCD的两边长为AB=6,BC=4,将矩形ABCD绕着点C顺时针旋转90°后,点A转到点A′的位置上,对角线AC扫过的面积是13π. 分析 根据长方形ABCD的两边长为AB=6,BC=4,可以求得对角戏AC的长,由矩形ABCD绕着点C顺时针旋转90°后,可知对角线AC扫过的面积正好是一个扇形,圆心角是90°,半径是AC的长,然后根据扇形的面积计算公式即可解答本题.
解答 解:由已知可得,
AB=6,BC=4,∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}=\sqrt{{6}^{2}+{4}^{2}}=\sqrt{52}=2\sqrt{13}$,
∵矩形ABCD绕着点C顺时针旋转90°
∴对角线AC扫过的面积是:$\frac{90×π×(2\sqrt{13})^{2}}{360}=13π$,
故答案为:13π.
点评 本题考查扇形面积的计算,解题的关键是明确扇形面积的计算公式,利用转化的数学思想进行解答.


科目:初中数学 来源: 题型:解答题
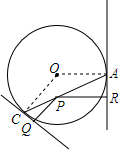 如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.
如图,设P为圆O内一定点,过P任作一弦AC,分别过A,C引圆的切线,再过P分别作两切线的垂线,垂足为Q,R.求证:$\frac{1}{PQ}$+$\frac{1}{PR}$为定值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ac<bc | B. | a2<b2 | C. | a+1<b+1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.
如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com