
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 首先根据非负数的性质确定a、b的值,然后确定其不经过的象限即可.
解答 解:∵(a+3)2+$\sqrt{2b-1}$=0,
∴a+3=0,2b-1=0,
解得:a=-3<0,b=$\frac{1}{2}$>0,
∴一次函数y=ax+b的图象经过一、二、四象限,
故选C.
点评 本题考查了一次函数的性质.一次函数y=kx+b的图象经过的象限由k、b的值共同决定,有六种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小;
⑤当k>0,b=0,函数y=kx+b的图象经过第一、三象限;
⑥当k<0,b=0,函数y=kx+b的图象经过第二、四象限.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
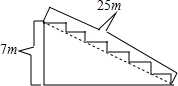 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.| A. | 21 | B. | 75 | C. | 93 | D. | 96 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
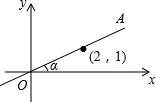 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3>b-3 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -3a>-3b | D. | 3a-1>3b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com