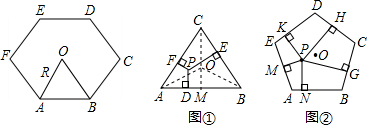
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
探索发现:
(1)为了解决这个问题,我们不妨从最简单的正多边形--正三角形入手.
如图①,△ABC是正三角形,半径OA=R,∠AOB是中心角,P是△ABC内任意一点,P到△ABC各边距离分别为h
1、h
2、h
3 ,确定h
1+h
2+h
3的值与△ABC的半径R及中心角的关系.
解:设△ABC的边长是a,面积为S,显然S=
a(h
1+h
2+h
3)
O为△ABC的中心,连接OA、OB、OC,它们将△ABC分成三个全等的等腰三角形,过点O作OM⊥AB,垂足为M,Rt△AOM中,易知
OM=OAcos∠AOM=Rcos
∠AOB=Rcos
×120°=Rcos60°,
AM=OAsin∠AOM=Rsin
∠AOB=Rsin
×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S
△AOB=
AB×OM=
×2Rsin60°•Rcos60°=R
2sin60°cos60°
∴S
△ABC=3S
△AOB=3R
2sin60°cos60°
∴
a(h
1+h
2+h
3)=3R
2sin60°cos60°
即:
×2Rsin60°(h
1+h
2+h
3)=3R
2sin60°cos60°
∴h
1+h
2+h
3=3Rcos60°
(2)如图②,五边形ABCDE是正五边形,半径是R,P是正五边形ABCDE内任意一点,P到五边形ABCDE各边距离分别为h
1、h
2、h
3、h
4、h
5,参照(1)的探索过程,确定h
1+h
2+h
3+h
4+h
5的值与正五边形ABCDE的半径R及中心角的关系.
(3)类比上述探索过程,直接填写结论
正六边形(半径是R)内任意一点P到各边距离之和 h
1+h
2+h
3+h
4+h
5+h
6=
6Rcos30°
6Rcos30°
正八边形(半径是R)内任意一点P到各边距离之和 h
1+h
2+h
3+h
4+h
5+h
6+h
7+h
8=
8Rcos22.5°
8Rcos22.5°
正n边形(半径是R)内任意一点P到各边距离之和 h
1+h
2+…+h
n=
.

 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?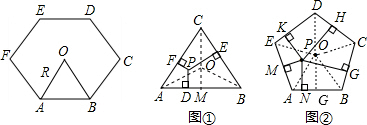 解:(2)设正五边形的边长是a,面积为S,显然S=
解:(2)设正五边形的边长是a,面积为S,显然S=

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案 (2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( )
(2012•青岛模拟)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则该圆的半径为( ) (2012•青岛模拟)如图,△ABC中,∠ACB=90°,如果将∠ABC沿BE对折,点C恰好落在AB边上的点D处,若AC=5cm,则AE+DE的值为
(2012•青岛模拟)如图,△ABC中,∠ACB=90°,如果将∠ABC沿BE对折,点C恰好落在AB边上的点D处,若AC=5cm,则AE+DE的值为