
 ,那么
,那么 等于 ( )
等于 ( )
A. | B.61° | C. | D. |
科目:初中数学 来源:不详 题型:填空题
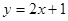 的图象与x轴交点的坐标为(
的图象与x轴交点的坐标为(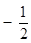 ,0),所以该函数的零点是
,0),所以该函数的零点是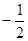 .
.
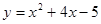 的零点是 ;
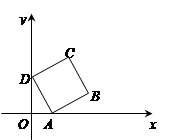
的零点是 ;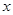 轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在
轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在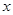 轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与
轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与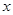 轴所围区域的面积为 .
轴所围区域的面积为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 )时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。
)时,设一直角边与x轴交于点E,另一直角边与y轴交于点F,在三角板绕点P旋转的过程中,使得△POE能否成为等腰三角形.请写出所有满足条件的点F的坐标 。
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.3种 | B.4种 | C.5种 | D.6种 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。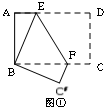
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
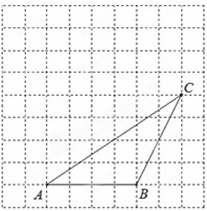
 的顶点都在格点上,且△
的顶点都在格点上,且△ 与△
与△ 关于点
关于点 成中心对称.
成中心对称.
 的位置;
的位置;  沿水平方向向右平移5个单位后的△
沿水平方向向右平移5个单位后的△ .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com