
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1 , 四边形EFQP的面积为S2 , 四边形PQCB的面积为S3 . 
(1)求证:EF+PQ=BC;
(2)若S1+S3=S2 , 求![]() 的值;
的值;
(3)若S3﹣S1=S2 , 直接写出![]() 的值.
的值.
【答案】
(1)
证明:∵EF∥BC,PQ∥BC,
∴![]() ,
,![]() ,
,
∵AE=BP,
∴AP=BE,
∴![]() =
=![]() =1,
=1,
∴![]() =1,
=1,
∴EF+PQ=BC;
(2)
解:过点A作AH⊥BC于H,分别交PQ于M、N,如图所示:
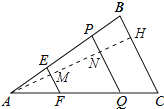
设EF=a,PQ=b,AM=h,
则BC=a+b,
∵EF∥PQ,
∴△AEF∽△APQ,
∴![]() =
=![]() ,
,
∴AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
∴S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,
(b+a+b)h,
∵S1+S3=S2,
∴![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=3a,
∴![]() =3,
=3,
∴![]() =2;
=2;
(3)
解:∵S3﹣S1=S2,
∴![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,
﹣1)h,
解得:b=(1±![]() )a(负值舍去),
)a(负值舍去),
∴b=(1+![]() )a,
)a,
∴![]() =1+
=1+![]() ,
,
∴![]() =
=![]() .
.
【解析】(1)由平行线得出比例式![]() ,
,![]() ,证出AP=BE,得出
,证出AP=BE,得出![]() =1,即可得出EF+PQ=BC;
=1,即可得出EF+PQ=BC;
(2)过点A作AH⊥BC于H,分别交PQ于M、N,设EF=a,PQ=b,AM=h,则BC=a+b,由平行线得出△AEF∽△APQ,得出![]() =
=![]() ,得出AN=
,得出AN=![]() ,MN=(
,MN=(![]() ﹣1)h,
﹣1)h,
由三角形的面积公式得出S1=![]() ah,S2=
ah,S2=![]() (a+b)(
(a+b)(![]() ﹣1)h,S3=
﹣1)h,S3=![]() (b+a+b)h,得出
(b+a+b)h,得出![]() ah+
ah+![]() (a+b+b)h=
(a+b+b)h=![]() (a+b)(
(a+b)(![]() ﹣1)h,求出b=3a,即可得出结果;(3)由题意得出
﹣1)h,求出b=3a,即可得出结果;(3)由题意得出![]() (a+b+b)h﹣
(a+b+b)h﹣![]() ah=
ah=![]() (a+b)(
(a+b)(![]() ﹣1)h,得出b=(1+
﹣1)h,得出b=(1+![]() )a,即可得出结果.
)a,即可得出结果.


科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是 . 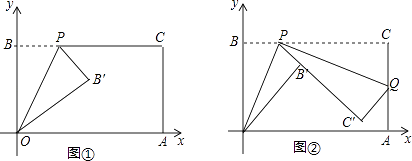
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0). 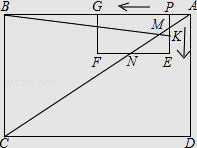
(1)当t=1时,KE= , EN=;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象,请回答下列问题:
![]() 试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
![]() 如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

查看答案和解析>>
科目:初中数学 来源: 题型:
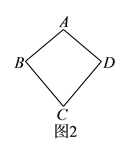
【题目】从图![]() 所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
具体定义如下:如图![]() ,在四边形
,在四边形![]() 中,
中, ![]() ,
, ![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.
,我们把这种两组邻边分别相等的四边形叫做“筝形”.

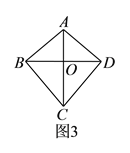
(![]() )结合图
)结合图![]() ,通过观察、测量、折纸,可以猜想“筝形”具有诸如“
,通过观察、测量、折纸,可以猜想“筝形”具有诸如“![]() 平分
平分![]() 和
和![]() ”这样的性质,请结合图形,再写出两条“筝形”的性质.
”这样的性质,请结合图形,再写出两条“筝形”的性质.
①____________________________.
②____________________________.
(![]() )从你写出的两条性质中,任选一条“筝形”的性质给出证明.
)从你写出的两条性质中,任选一条“筝形”的性质给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,完全平方式可以用平面几何图形的面积来表示。实际上还有一些代数恒等式也可以用这种形式表示,如:(2a+b)(a+b)=2a2+3ab+b2,就可以用图(1)或图(2)等图形的面积表示。

(1)请写出图(3)所表示的代数恒等式: ;
(2)试画一个几何图形,使它的面积表示:(a+b)(a+2b)=a2+3ab+2b2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究 探索:在如图1至图3中,△ABC的面积为a .
(1)如图1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);




(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com