
分析 此题要分两种情况进行讨论:(1)当等腰三角形的顶角是钝角时,腰上的高在三角形的外部,先在Rt△ACO中由勾股定理求出AO=4,于是OB=AB+AO=9,然后在Rt△BCO中利用勾股定理即可求出BC即可;
(2)当等腰三角形的顶角是锐角时,腰上的高在三角形的内部,在Rt△ACO中由勾股定理求出AD=4,于是DB=AB-AD=1,然后在Rt△BCD中利用勾股定理求出BC即可.
解答 解:分两种情况: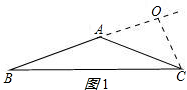
(1)顶角是钝角时,如图1所示:
在Rt△ACO中,由勾股定理,得AO2=AC2-OC2=52-32=16,
∴AO=4,
OB=AB+AO=5+4=9,
在Rt△BCO中,由勾股定理,得BC2=OB2+OC2=92+32=90,
∴BC=$\sqrt{90}$=3$\sqrt{10}$;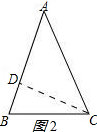
(2)顶角是锐角时,如图2所示:
在Rt△ACD中,由勾股定理,得AD2=AC2-DC2=52-32=16,
∴AD=4,
DB=AB-AD=5-4=1.
在Rt△BCD中,由勾股定理,得BC2=DB2+DC2=12+32=10,
∴BC=$\sqrt{10}$;
综上可知,这个等腰三角形的底的长度为3$\sqrt{10}$或$\sqrt{10}$.
故答案为:3$\sqrt{10}$或$\sqrt{10}$.
点评 本题考查了勾股定理及等腰三角形的性质,难度适中,分情况讨论是解题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
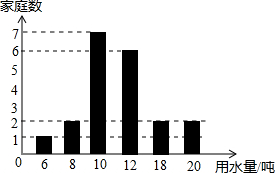 某校八年级去年12月份开展了家庭用水量调查活动,并约定:如果12月份的用水量在“选定标准”的±20%范围之内都称为“普通用水量”.现随机选出该年级20名学生,将其家庭12月份的用水量情况进行统计并绘制成如下统计图,请根据统计图信息解决问题:
某校八年级去年12月份开展了家庭用水量调查活动,并约定:如果12月份的用水量在“选定标准”的±20%范围之内都称为“普通用水量”.现随机选出该年级20名学生,将其家庭12月份的用水量情况进行统计并绘制成如下统计图,请根据统计图信息解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
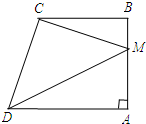 如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.
如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
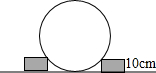 某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程.
某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com