练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′．

    （1）在坐标纸上画出这几次变换相应的图形；

     


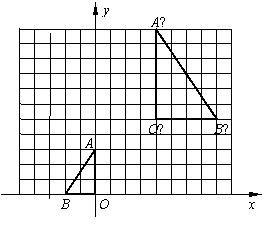
    （2）设P（x，y）为△OAB边上任一点，依次写出这几次变换后点P对应点的坐标．

    解：

    （1）

     


    （2）设坐标纸中方格边长为单位1，则

    P（x，y）（2x，2y）（2x，2y）（，2y）（，）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
    对上述命题证明如下：
    证明：连接OC
    ∵OA=OC
    ∴∠A=∠1
    ∵CD切O于C点
    ∴∠OCD=90°
    ∴∠1+∠2=90°
    ∴∠A+∠2=90°
    在Rt△QPA中，∠QPA=90°
    ∴∠A+∠Q=90°
    ∴∠2=∠Q
    ∴DQ=DC
    即CDQ是等腰三角形．
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第35章《圆（二）》中考题集（17）：35.3 探索切线的性质（解析版） 题型：解答题

    已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
    对上述命题证明如下：
    证明：连接OC
    ∵OA=OC
    ∴∠A=∠1
    ∵CD切O于C点
    ∴∠OCD=90°
    ∴∠1+∠2=90°
    ∴∠A+∠2=90°
    在Rt△QPA中，∠QPA=90°
    ∴∠A+∠Q=90°
    ∴∠2=∠Q
    ∴DQ=DC
    即CDQ是等腰三角形．
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第28章《圆》中考题集（50）：28.2 与圆有关的位置关系（解析版） 题型：解答题

    已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
    对上述命题证明如下：
    证明：连接OC
    ∵OA=OC
    ∴∠A=∠1
    ∵CD切O于C点
    ∴∠OCD=90°
    ∴∠1+∠2=90°
    ∴∠A+∠2=90°
    在Rt△QPA中，∠QPA=90°
    ∴∠A+∠Q=90°
    ∴∠2=∠Q
    ∴DQ=DC
    即CDQ是等腰三角形．
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第3章《直线与圆、圆与圆的位置关系》中考题集（16）：3.1 直线与圆的位置关系（解析版） 题型：解答题

    已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
    对上述命题证明如下：
    证明：连接OC
    ∵OA=OC
    ∴∠A=∠1
    ∵CD切O于C点
    ∴∠OCD=90°
    ∴∠1+∠2=90°
    ∴∠A+∠2=90°
    在Rt△QPA中，∠QPA=90°
    ∴∠A+∠Q=90°
    ∴∠2=∠Q
    ∴DQ=DC
    即CDQ是等腰三角形．
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：第3章《圆》中考题集（44）：3.5 直线和圆的位置关系（解析版） 题型：解答题

    已知：如图，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D．则△CDQ是等腰三角形．
    对上述命题证明如下：
    证明：连接OC
    ∵OA=OC
    ∴∠A=∠1
    ∵CD切O于C点
    ∴∠OCD=90°
    ∴∠1+∠2=90°
    ∴∠A+∠2=90°
    在Rt△QPA中，∠QPA=90°
    ∴∠A+∠Q=90°
    ∴∠2=∠Q
    ∴DQ=DC
    即CDQ是等腰三角形．
    问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图所示，结论“△CDQ是等腰三角形”还成立吗？若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案