
分析 (1)根据“互为谐角”的定义列出算式计算即可求解;
(2)可设这个角的度数是x,根据等量关系:一个角的补角=这个角的谐角×5,列出方程求解即可;
(3)根据角平分线的定义得到∠EOF=60°,再根据“互谐”的定义即可求解.
解答 解:(1)26°5′的谐角=60°-26°5′=33°55′;
(2)设这个角的度数是x,依题意有
180°-x=5(60°-x),
解得x=30°.
故这个角的度数是30°;
(3)∵OE,OF分别平分∠AOC,∠BOC,
∴∠AOE=∠COE=$\frac{1}{2}$∠AOC,∠BOF=∠COF=$\frac{1}{2}$∠BOC,
∵∠AOB=120°,
∴∠AOE+∠COF=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=60°,
∴∠AOE+∠BOF=60°,∠COE+∠BOF=60°,∠COE+∠COF=60°,
∴互谐的角有∠AOE和∠COF,∠AOE和∠BOF,∠COE和∠BOF,∠COE和∠COF.
点评 本题考查了余角和补角,角平分线定义,学生的阅读理解能力及知识的迁移能力.理解互为谐角的定义是解题的关键.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
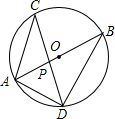 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=45°,∠APD=75°.
如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=45°,∠APD=75°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com