
 解:①5是腰长时,由勾股定理得,AD=
解:①5是腰长时,由勾股定理得,AD=| 52-32 |
| 32+12 |
| 10 |
| 10 |
| 10 |
| 32+92 |
| 10 |
| 10 |
| 10 |
| 52-32 |
| 1 |
| 2 |
| 5 |
| 2 |
| BE |
| AB |
| BD |
| BC |
| ||
| AB |
| 4 |
| 5 |
| 25 |
| 8 |
| 25 |
| 8 |
| 45 |
| 4 |
| 10 |
| 10 |
| 45 |
| 4 |
| 10 |
| 10 |
| 45 |
| 4 |


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
 某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面:
某商场举行店庆酬宾促销活动,商场规定:顾客每购买99元的商品,就能获得一次抽奖的机会,如果顾客不愿意抽奖,可以直接获得购物券10元.商场内设立了多个抽奖点,为了吸引顾客商场电子屏实时显示抽奖状况,下面是一位顾客用手机拍下的电子屏画面:查看答案和解析>>
科目:初中数学 来源: 题型:
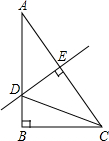 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AD的长是( )
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD,若BD=1,则AD的长是( )A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com