a,b,c是非负数,且3a+2b+c=5,2a+b-3c=1,设m=3a+b-7c,m的最小值是x,m的最大值是y,则xy=?
解:∵3a+2b+c=5(1),2a+b-3c=1(2),
(1)-(2)×2得,-a+7c=3,即a=7c-3,
∴代入(2)得b=1-2a+3c=1-2(7c-3)+3c=-11c+7,
∵a≥0,b≥0,c≥0,
∴7c-3≥0,c≥

,
∴-11c+7≥0,c≤

,
∴

≤c≤

,
∴M=3a+b-7c=3(7c-3)+(-11c+7)-7c=3c-2,
当c=

时,M有最小值:x=3×

-2=-

,
当c=

时,M有最大值:y=3×

-2=-

.
∴xy=(-

)×(-

)=
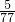
.
故答案为:
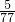
.
分析:先把已知两代数式联立,用c表示出a、b的值,再根据a,b,c是非负数即可求出c的取值范围,再用c表示出M的值,根据c的取值范围即可求出x、y的值,再代入xy进行计算即可.
点评:本题考查的是一次函数的性质,解答此题的关键是把c当作已知表示出a、b的值,再求出c的取值范围.

 ,
, ,
, ≤c≤
≤c≤ ,
, 时,M有最小值:x=3×
时,M有最小值:x=3× -2=-
-2=- ,
, 时,M有最大值:y=3×
时,M有最大值:y=3× -2=-
-2=- .
. )×(-
)×(- )=
)=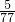 .
.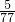 .
.

 名校课堂系列答案
名校课堂系列答案