Question

已知抛物线y=ax²+bx经过点A（2，0），顶点为D（1，-1）．
（1）确定抛物线的解析式；
（2）直线y=3与抛物线相交于B、C两点（B点在C点左侧），以BC为一边，原点O为另一顶点作平行四边形，设平行四边形的面积为S，求S的值；
（3）若以（2）小题中BC为一边，抛物线上的任一点P为另一顶点作平行四边形，当平行四边形面积为8时，试确定P点的坐标；
（4）当-2≤x≤4时，（3）小题中平行四边形的面积是否有最大值？若有请求出，若无请说明理由．

Answer 1

分析：（1）将A，D两点的坐标代入抛物线中，即可得出抛物线的解析式．
（2）先根据抛物线的解析式求出B，C两点的坐标，进而得出BC的长，然后根据B点的纵坐标（即平行四边形的高），求出S的值．
（3）由于BC边的长已确定，因此可根据平行四边形的面积求出P点和B点的纵坐标差的绝对值，以此可得出P点的纵坐标，然后根据抛物线的解析式即可求出P点的坐标．
（4）先根据抛物线的解析式找出x在-2和4区间抛物线上到BC距离最长的点，进而可求出平行四边形的最大面积．

解答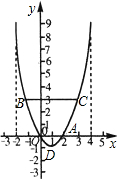：解：（1）∵抛物线y=ax²+bx过点A（2，0），D（1，-1），
∴

4a+2b=0 a+b=-1

解得a=1，b=-2．
则抛物线的解析式为y=x²-2x．

（2）在抛物线解析式为y=x²-2x中，令y=3，
即3=x²-2x．
解得x₁=-1，x₂=3
则B（-1，3）、C（3，3）．
故BC=4，那么S=4×3=12．

（3）当P点在直线BC下方时，
S=4×（3-y）=12-4y=8，y=1．
由x²-2x=1，得：
x1=1-

2

，x2=1+

2

．
则P点的坐标为
P₁（1-

2

，1），P₂（1+

2

，1）．
当P点在直线BC上方时，
S=4×（y-3）=4y-12=8，y=5．
由x²-2x=5，得：
x3=1-

6

，x4=1+

6

．
则P点的坐标为
P₃（1-

6

，5），P₄（1+

6

，5）．

（4）把x=-2代入y=x²-2x，
得y=8，
把x=4代入y=x²-2x，
得y=8，
当-2≤x≤4时，顶点D到BC的距离为4，抛物线上与线段BC距离最远的有两个点，坐标分别为（-2，8）、（4，8）与线段BC的距离都为5．
∴S有最大值，其最大值为
S=4×（8-3）=20．

点评：本题主要考查二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力．