
如图,南北方向PQ以东为我国的领海,以西为公海.某天晚上10时28分,我边防反偷渡巡逻艇101号在A处发现其正西方向的C处有一可疑船只正向我沿海靠近,便立即通知正在PQ上B处巡逻的103号艇注意其动向.经观测发现,A、C之间的距离为10海里,A、B之间的距离为6海里,B、C之间的距离为8海里.若该可疑船只的速度为12.8海里/时,则该可疑船只最早在何时进入我国领海?

|
分析:要求该船只最早何时进入我国领海,必先确定该船只进入我国领海的航线.由“垂线段最短”可知,CD的长即为该船只进入我国领海的最短距离.在与方位有关的应用题中,南北方向线与东西方向线互相垂直,正确运用这一条件,结合勾股定理及其逆定理来解决此类问题 解:设PQ与AC交于点D,则∠CDB=90°. 因为AB=6海里,BC=8海里,AC=10海里, 所以AB2+BC2=AC2. 所以△BAC为直角三角形,且∠ABC=90°. 因为BD⊥AC于点D, 所以可疑船只进入我国领海的最近距离为CD的长. 又因为S△ABC= 所以6×8=10·BD.解得BD= 在Rt△BCD中,∠BDC=90°, 所以CD2=BC2-BD2=82-( 所以CD= 所以从C到D所需的时间为 6.4÷12.8=0.5(小时)=30(分). 所以可疑船只最早在10时58分进入我国领海. |


科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:
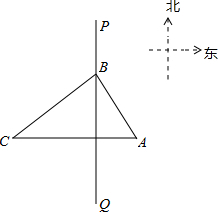 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第9期 总第165期 华师大版 题型:044
如图,南北方向MN以西为我国领海,以东为公海.某天上午9时50分,我国反走私艇A发现正东方向有一走私艇C正以13海里/时的速度偷偷向我国领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得离走私艇C的距离是12海里.若走私艇C的速度不变,大约最早会在什么时间进入我国领海?
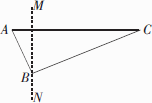
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
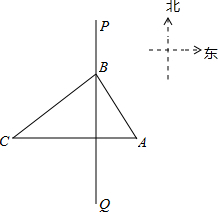 B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?
B=6海里,BC=8海里,若该船只的速度为12.8海里/小时,则可疑船只最早何时进入我领海?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com